Giải mục 2 trang 22, 23 SGK Toán 11 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 22, 23 SGK Toán 11 tập 2. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.

tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.

Ta biết: Với (C1) là đồ thị của hàm số y = f(x) và (C2) là đồ thị của hàm số y = g(x)

Hoạt động 2

Ta biết: Với (C₁) là đồ thị của hàm số y = f(x) và (C₂) là đồ thị của hàm số y = g(x) thì tập hợp giá trị của x để (C₁) nằm phía trên (C₂) là tập nghiệm của bất phương trình f(x) > g(x).

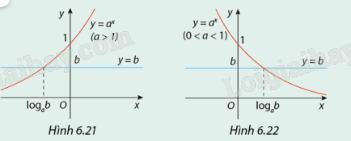
Quan sát các đồ thị (Hình 6.21 và 6.22) trong Hoạt động 1 và trong mỗi trường hợp, hãy tìm các tập nghiệm của bất phương trình a^x > b:

a) Khi b > 0;

b) Khi b ≤ 0.

Giải mục 2 trang 22, 23 SGK Toán 11 tập 2 - Cùng khám phá 1

Phương pháp giải:

Quan sát hình vẽ.

Lời giải chi tiết:

a) Khi b > 0:

a > 1: a^x > b \( \Leftrightarrow x > {\log _a}b\)

0 < a < 1: a^x > b \( \Leftrightarrow x < {\log _a}b\)

b) Khi b ≤ 0 thì bất phương trình nghiệm đúng với mọi \(x \in \mathbb{R}\).

Luyện tập 2

Giải các bất phương trình sau:

a) \({2^{x + 1}} > {2^{3x + 5}}\)

b) \({\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}\)

Phương pháp giải:

Khi a > 1: \({a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) > B\left( x \right)\)

Khi 0 < a < 1: \({a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) < B\left( x \right)\)

Lời giải chi tiết:

\(\begin{array}{l}{2^{x + 1}} > {2^{3x + 5}}\\ \Leftrightarrow x + 1 > 3x + 5\\ \Leftrightarrow - 2x > 4\\ \Leftrightarrow x < - 2\end{array}\)

Vậy tập nghiệm của bất phương trình đã cho là \(\left( { - \infty ; - 2} \right)\).

\(\begin{array}{l}{\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}\\ \Leftrightarrow {\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le {\left( {\frac{7}{9}} \right)^{ - 1}}\\ \Leftrightarrow 2{x^2} - 3x \ge - 1\\ \Leftrightarrow 2{x^2} - 3x + 1 \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le \frac{1}{2}\end{array} \right.\end{array}\)

Vậy tập nghiệm của bất phương trình đã cho là \(\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right)\).

Giải mục 2 trang 22, 23 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải

Mục 2 trang 22, 23 SGK Toán 11 tập 2 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình học.

1. Nội dung chính của Mục 2

Phép tịnh tiến: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép tịnh tiến.
Phép quay: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép quay.
Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng trục.
Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng tâm.

2. Phương pháp giải bài tập

Để giải các bài tập trong mục này, các em cần:

Nắm vững định nghĩa và tính chất của từng phép biến hình.
Xác định chính xác các yếu tố của phép biến hình (ví dụ: vectơ tịnh tiến, tâm quay, trục đối xứng, tâm đối xứng).
Sử dụng các công thức và quy tắc để tính toán tọa độ của ảnh.
Vẽ hình minh họa để trực quan hóa bài toán.

3. Ví dụ minh họa và lời giải chi tiết

Bài 1: Cho điểm A(1; 2) và vectơ tịnh tiến v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v.

Lời giải:

Áp dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)

Ta có: A'(1 + 3; 2 - 1) = A'(4; 1)

Bài 2: Cho đường tròn (C) có tâm I(2; -3) và bán kính r = 5. Tìm phương trình đường tròn (C') là ảnh của (C) qua phép quay tâm O(0; 0) góc 90 độ.

Lời giải:

Phép quay tâm O góc 90 độ biến điểm M(x; y) thành điểm M'( -y; x). Do đó, tâm I(2; -3) của (C) biến thành I' (3; 2).

Bán kính của (C') bằng bán kính của (C), tức là r' = 5.

Vậy phương trình đường tròn (C') là: (x - 3)^2 + (y - 2)^2 = 25

4. Luyện tập và củng cố kiến thức

Để củng cố kiến thức, các em nên tự giải thêm các bài tập trong SGK và các đề thi thử. tusach.vn cung cấp đầy đủ các tài liệu tham khảo và bài tập luyện tập để giúp các em đạt kết quả tốt nhất trong môn Toán.

5. Mở rộng kiến thức

Các em có thể tìm hiểu thêm về ứng dụng của các phép biến hình trong thực tế, ví dụ như trong thiết kế đồ họa, kiến trúc, và các lĩnh vực khoa học khác.

Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Giải mục 2 trang 22, 23 SGK Toán 11 tập 2. Chúc các em học tập tốt!

Giải mục 2 trang 22, 23 SGK Toán 11 tập 2 - Cùng khám phá