Giải mục 1 trang 81, 82 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 81, 82 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 81, 82 SGK Toán 11 tập 1 trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
Dòng 1 của bảng dưới đây cho biết biểu thức của một hàm số. Dòng 2 cho biết đồ thị của hàm số đã cho. Trả lời các câu hỏi ở dòng 3 và 4
Hoạt động 1
Dòng 1 của bảng dưới đây cho biết biểu thức của một hàm số. Dòng 2 cho biết đồ thị của hàm số đã cho. Trả lời các câu hỏi ở dòng 3 và 4
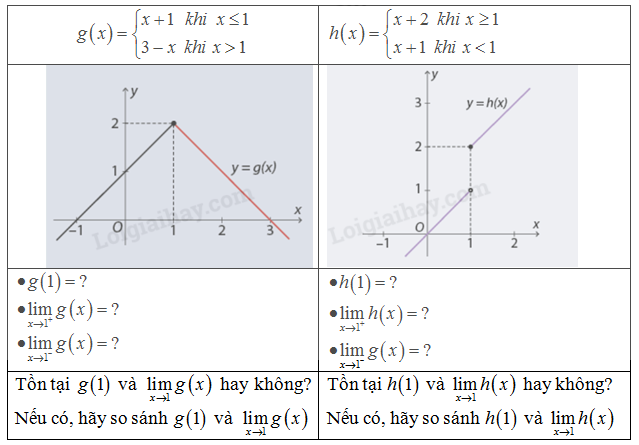
Phương pháp giải:
Với \(x = 1\) nên dựa vào điều kiện \(x \le 1\) để tính \(g\left( 1 \right)\) thì thay vào hàm số \(g\left( x \right) = x + 1\)
Với \(h\left( 1 \right)\) tính tương tự như \(g\left( 1 \right)\)
Khi \(x \to {1^ + }\) tức là \(x \ge 1\) nên phải tính\(\,\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)\) ứng với hàm số \(g\left( x \right) = x + 1\)
Còn khi \(x \to {1^ - }\) tức là \(x < 1\) nên phải tính \(\,\mathop {\lim }\limits_{x \to {1^ - }} g\left( x \right)\) ứng với hàm số \(g\left( x \right) = 3 - x\)
Hàm \(h\left( x \right)\) thì làm tương tự như hàm \(g\left( x \right)\)
Lời giải chi tiết:

Luyện tập 1
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - x - 6}}{{x + 2}}\,\,\,khi\,\,x \ne 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 6\,\,\,khi\,\,x = - 2\end{array} \right.\). Xét tính liên tục của hàm số tại \({x_0} = - 2\)
Phương pháp giải:
Hàm số liên tục tại \({x_0} = - 2\) nếu \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = f\left( { - 2} \right)\)
Đây là giới hạn tại điểm dạng vô định \(\frac{0}{0}\) nên phải thực hiện khử mẫu
Đây là hàm phân thức hữu tỉ nên ta thực hiện phân tích đa thức thành nhân tử để khử dạng vô định
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Khi \(x = - 2\), ta có \(f\left( { - 2} \right) = - 6\)
\(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{\left( {x + 2} \right)\left( {x - 3} \right)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \left( {x - 3} \right) = - 2 - 3 = - 5\)
Vì \( - 5 \ne - 6\) \( \Rightarrow \) \(\mathop {\lim }\limits_{x \to - 2} f\left( x \right) \ne f\left( { - 2} \right)\) do đó hàm số không liên tục tại \({x_0} = - 2\)
Hoạt động 2
Xét tính liên tục của hàm số \(f\left( x \right) = {x^2} + 1\) tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)
Phương pháp giải:
Hàm số liên tục tại \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Khi \(x = {x_0}\) thì \(f\left( {{x_0}} \right) = x_0^2 + 1\)
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + 1} \right) = x_0^2 + 1 = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0}\) bất kì thuộc \(\mathbb{R}\)
Luyện tập 2
Xét tính liên tục của hàm số \(f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\)
Phương pháp giải:
Hàm số liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Lời giải chi tiết:
Hàm số có tập xác định là \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\)
Với mọi \({x_0} > 1\), ta có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} - 1}}{{x - 1}} = \frac{{x_0^2 - 1}}{{{x_0} - 1}} = f\left( {{x_0}} \right)\). Vậy hàm số liên tục tại mọi điểm \({x_0} > 1\) nên hàm số liên tục trên \(\left( {1; + \infty } \right)\)
Giải mục 1 trang 81, 82 SGK Toán 11 tập 1: Tổng quan và Phương pháp giải
Mục 1 trang 81, 82 SGK Toán 11 tập 1 tập trung vào việc ôn tập chương 1: Hàm số lượng giác và đồ thị. Đây là phần kiến thức nền tảng quan trọng cho các chương tiếp theo. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập trong mục này sẽ giúp các em tự tin hơn khi đối mặt với các bài toán phức tạp hơn.
Nội dung chính của Mục 1
- Ôn tập lý thuyết: Các khái niệm về hàm số lượng giác (sin, cos, tan, cot), tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị hàm số lượng giác.
- Bài tập vận dụng: Các bài tập liên quan đến việc xác định tập xác định, tập giá trị, tìm chu kỳ, vẽ đồ thị hàm số lượng giác, giải phương trình lượng giác cơ bản.
- Bài tập nâng cao: Các bài tập đòi hỏi sự kết hợp kiến thức và kỹ năng, thường liên quan đến việc biến đổi phương trình lượng giác, sử dụng tính chất của hàm số lượng giác để giải quyết các bài toán thực tế.
Giải chi tiết các bài tập trong Mục 1
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 81, 82 SGK Toán 11 tập 1:
Bài 1: (Trang 81)
Đề bài: Xác định tập xác định của hàm số y = √(2 - sinx)
Lời giải:
Hàm số y = √(2 - sinx) xác định khi và chỉ khi 2 - sinx ≥ 0. Vì -1 ≤ sinx ≤ 1 nên 2 - sinx ≥ 2 - 1 = 1 > 0 với mọi x. Vậy tập xác định của hàm số là R.
Bài 2: (Trang 81)
Đề bài: Tìm chu kỳ của hàm số y = sin(2x + π/3)
Lời giải:
Chu kỳ của hàm số y = sin(ax + b) là T = 2π/|a|. Trong trường hợp này, a = 2, b = π/3. Vậy chu kỳ của hàm số y = sin(2x + π/3) là T = 2π/2 = π.
Bài 3: (Trang 82)
Đề bài: Vẽ đồ thị hàm số y = cosx trên đoạn [-π; π]
Lời giải:
Để vẽ đồ thị hàm số y = cosx trên đoạn [-π; π], ta có thể lập bảng giá trị:
| x | y = cosx |
|---|---|
| -π | -1 |
| -π/2 | 0 |
| 0 | 1 |
| π/2 | 0 |
| π | -1 |
Dựa vào bảng giá trị, ta vẽ được đồ thị hàm số y = cosx trên đoạn [-π; π].
Mẹo giải bài tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ các khái niệm, định nghĩa, tính chất và công thức liên quan đến hàm số lượng giác.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác các giá trị lượng giác.
- Tham khảo các nguồn tài liệu: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến, video bài giảng...
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!