Giải mục 2 trang 83, 84 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 83, 84 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 83, 84 SGK Toán 11 tập 1. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích kỹ lưỡng từng câu hỏi, đảm bảo các em hiểu rõ bản chất vấn đề.
Các hàm số \(f\left( x \right) = {x^3} - 3x + 2\) và \(g\left( x \right) = \sin x\) xác định trên \(\left( { - \infty ; + \infty } \right)\) có đồ thị như sau:
Hoạt động 3
Các hàm số \(f\left( x \right) = {x^3} - 3x + 2\) và \(g\left( x \right) = \sin x\) xác định trên \(\left( { - \infty ; + \infty } \right)\) có đồ thị như sau:
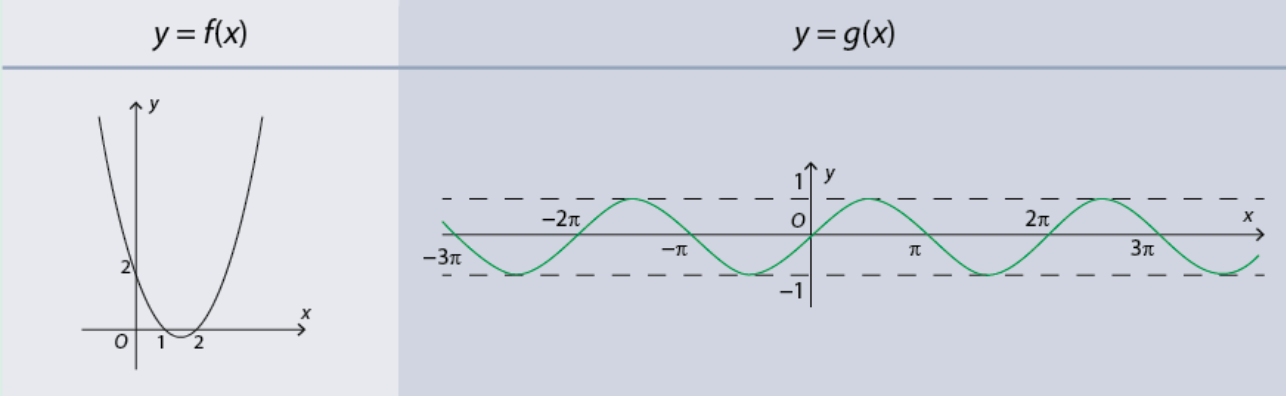
Dựa vào đồ thị, hãy dự đoán tính liên tục của các hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) trên \(\left( { - \infty ; + \infty } \right)\).
Phương pháp giải:
Đồ thị hàm số liên tục trên một khoảng là đường liền trên khoảng đó
Lời giải chi tiết:
Quan sát đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) ta thấy chúng là một đường nét liền trên \(\left( { - \infty ; + \infty } \right)\) nên hai hàm số đó liên tục trên \(\left( { - \infty ; + \infty } \right)\)
Luyện tập 3
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} + x - 2}}{{x - 1}}\,\,\,khi\,\,x \ne 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,khi\,\,x = 1\end{array} \right.\) trên \(\mathbb{R}\)
Phương pháp giải:
Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Hàm số phân thức hữu tỉ (thương của hai đa thức) liên tục trên từng khoảng xác định của chúng.
Xét tính liên tục của hàm số \(f\left( x \right)\) tại điểm \(x = 1\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
+ Trên tập \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\), hàm số \(f\left( x \right) = \frac{{{x^3} + x - 2}}{{x - 1}}\) là phân thức hữu tỉ xác định trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) nên liên tục trên các khoảng này.
+ Khi \(x = 1\), ta có \(f\left( 1 \right) = 2\).
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} + x - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 2} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 2} \right) = {1^2} + 1 + 2 = 4 \ne f\left( 1 \right)\)
Vậy hàm số \(f\left( x \right)\) không liên tục tại \(x = 1\)
Suy ra hàm số đã cho gián đoạn tại \(x = 1\) hay hàm số \(f\left( x \right)\) không liên tục trên \(\mathbb{R}\)
Hoạt động 4
Cho hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = \frac{1}{x}\).
a) Xét tính liên tục của \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tại \({x_0} = 1\).
b) Xét tính liên tục của hàm số \(y = f\left( x \right) + g\left( x \right)\) tại \({x_0} = 1\).
Phương pháp giải:
Hàm số liên tại tại điểm \(x = {x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Tính \(f\left( {{x_0}} \right)\) và \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) rồi so sánh chúng
Tương tự với hàm \(y = g\left( x \right)\) và \(y = f\left( x \right) + g\left( x \right)\)
Lời giải chi tiết:
a)
+ Hàm số \(y = f\left( x \right) = {x^2}\) có TXĐ là \(\mathbb{R}\)
Với \({x_0} = 1 \Rightarrow f\left( 1 \right) = {1^2} = 1\)
\(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} {x^2} = {1^2} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
+ Hàm số \(y = g\left( x \right) = \frac{1}{x}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\)
Với \({x_0} = 1 \Rightarrow g\left( 1 \right) = \frac{1}{1} = 1\)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{1}{x} = \frac{1}{1} = 1 = f\left( 1 \right)\). Suy ra, hàm số \(y = f\left( x \right)\) liên tục tại \({x_0} = 1\)
b) Với \({x_0} = 1 \Rightarrow f\left( 1 \right) + g\left( 1 \right) = {1^2} + \frac{1}{1} = 2\)
\(\mathop {\lim }\limits_{x \to 1} \left( {f\left( x \right) + g\left( x \right)} \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + \frac{1}{x}} \right) = {1^2} + \frac{1}{1} = 2 = f\left( 1 \right) + g\left( 1 \right)\).
Suy ra, hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \({x_0} = 1\)
Luyện tập 4
Tìm các khoảng trên đó hàm số sau đây là liên tục: \(y = x + \tan x\)
Phương pháp giải:
Hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là các hàm số liên tục trên khoảng K thì hàm số \(y = f\left( x \right) \pm g\left( x \right)\) cũng liên tục trên khoảng K
Hàm số \(y = \tan x,y = \cot x\) liên tục trên từng khoảng xác định của chúng
Tìm tập xác định của hàm số
Lời giải chi tiết:
Xét hàm số \(f\left( x \right) = x\) và \(g\left( x \right) = \tan x\)
+ Hàm số \(f\left( x \right) = x\) là hàm đa thức nên \(f\left( x \right)\) liên tục trên \(\mathbb{R}\)
+ Hàm số \(g\left( x \right) = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) nên hàm số \(g\left( x \right)\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Do đó, hàm số \(y = f\left( x \right) + g\left( x \right) = x + \tan x\) liên tục trên các khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right)\)
Vận dụng
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,khi\,\,x \le 0\\ax + b\,\,khi\,\,0 < x < 2\\4 - x\,\,\,khi\,\,2 \le x\end{array} \right.\), trong đó \(a\) và \(b\) là hai số thực. Tìm \(a\) và \(b\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Phương pháp giải:
Hàm số liên tục trên \(\mathbb{R}\) nếu nó liên tục tại mọi điểm thuộc \(\mathbb{R}\)
Dựa tính liên tục tại các điểm \(x = 0;x = 2\) để tìm \(a\) và \(b\)
Lời giải chi tiết:
Tập xác định của hàm số là \(\mathbb{R}\)
Với \(x < 0\), hàm số \(f\left( x \right) = x + 1\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( { - \infty ;0} \right)\)
Với \(0 < x < 2\), hàm số \(f\left( x \right) = ax + b\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( {0;2} \right)\)
Với \(x > 2\), hàm số \(f\left( x \right) = 4 - x\) là hàm đa thức nên hàm số liên tục trên khoảng \(\left( {2; + \infty } \right)\)
Để hàm số liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại các điểm \(x = 0\) và \(x = 2\)
+ Với \(x = 0 \Rightarrow f\left( 0 \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {x + 1} \right) = 0 + 1 = 1\)
\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {ax + b} \right) = a.0 + b = b\)
Để hàm số liên tục tại \(x = 0\) thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow b = 1\) \(\left( 1 \right)\)
+ Với \(x = 2 \Rightarrow f\left( 2 \right) = 4 - 2 = 2\)
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {ax + b} \right) = 2a + b\)
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {4 - x} \right) = 4 - 2 = 2\)
Để hàm số liên tục tại \(x = 2\) thì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right) \Leftrightarrow 2a + b = 2\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(\left\{ \begin{array}{l}b = 1\\2a + b = 2\end{array} \right. \Leftrightarrow a = \frac{1}{2};b = 1\)
Giải mục 2 trang 83, 84 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình học.
Nội dung chính của Mục 2 trang 83, 84
- Phép tịnh tiến: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép tịnh tiến.
- Phép quay: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép quay.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng trục.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng tâm.
Phương pháp giải bài tập Mục 2
- Hiểu rõ định nghĩa và tính chất: Đây là bước quan trọng nhất để giải quyết bất kỳ bài toán nào.
- Xác định phép biến hình: Xác định chính xác phép biến hình nào được sử dụng trong bài toán.
- Áp dụng công thức: Sử dụng các công thức liên quan đến phép biến hình để tìm ra kết quả.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn phù hợp với điều kiện của bài toán.
Giải chi tiết các bài tập trang 83, 84
Bài 1: (Trang 83)
Đề bài: Cho điểm A(1; 2) và vector v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vector v.
Giải:
Tọa độ điểm A' được tính theo công thức: A'(xA + xv; yA + yv) = (1 + 3; 2 - 1) = (4; 1).
Bài 2: (Trang 84)
Đề bài: Cho đường tròn (C) có tâm I(2; -3) và bán kính r = 5. Tìm phương trình đường tròn (C') là ảnh của (C) qua phép quay tâm O(0; 0) góc 90o.
Giải:
Phép quay tâm O(0; 0) góc 90o biến điểm I(2; -3) thành điểm I'(-3; 2). Do đó, đường tròn (C') có tâm I'(-3; 2) và bán kính r = 5. Phương trình đường tròn (C') là: (x + 3)2 + (y - 2)2 = 25.
Bài tập tương tự và luyện tập
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
- Tìm ảnh của một điểm qua phép đối xứng trục.
- Tìm ảnh của một đường thẳng qua phép đối xứng tâm.
- Chứng minh một hình là ảnh của một hình khác qua một phép biến hình.
Lời khuyên
Hãy dành thời gian ôn tập lý thuyết và làm nhiều bài tập để nắm vững kiến thức về phép biến hình. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt!
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | A'(xA + xv; yA + yv) |
| Quay | (Công thức phức tạp hơn, tùy thuộc vào góc quay) |