Bài 4.25 trang 119 SGK Toán 11 tập 1
Bài 4.25 thuộc chương trình học Toán 11 tập 1, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
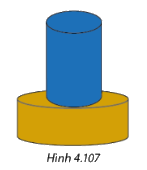
Một đồ chơi cấu tạo gồm hai hình trụ đặt chồng lên nhau như Hình 4.107, hình trụ ở trên có bán kính bằng một nửa bán kính của hình trụ ở dưới và chiều cao gấp đôi chiều cao của hình trụ ở dưới.
Bài 4.25 Trang 119 SGK Toán 11 Tập 1: Giải Chi Tiết và Phân Tích
Bài 4.25 trang 119 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bài tập này thường yêu cầu học sinh tìm đạo hàm của hàm số, xác định các điểm cực trị và khảo sát hàm số.
Nội dung bài tập 4.25
Thông thường, bài 4.25 sẽ đưa ra một hàm số cụ thể và yêu cầu:
- Tính đạo hàm f'(x) của hàm số.
- Tìm các điểm cực trị của hàm số (xác định các giá trị x sao cho f'(x) = 0 hoặc không xác định).
- Xác định loại cực trị (cực đại, cực tiểu) bằng cách sử dụng dấu của đạo hàm cấp hai f''(x) hoặc xét dấu của f'(x) xung quanh các điểm cực trị.
- Tìm giá trị cực đại, cực tiểu của hàm số.
Lời giải chi tiết bài 4.25 (Ví dụ minh họa)
Giả sử hàm số được cho là: f(x) = x3 - 3x2 + 2
- Tính đạo hàm f'(x):
f'(x) = 3x2 - 6x
- Tìm các điểm cực trị:
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
- Xác định loại cực trị:
Tính đạo hàm cấp hai: f''(x) = 6x - 6
Tại x = 0: f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
Tại x = 2: f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
- Tìm giá trị cực đại, cực tiểu:
f(0) = 2 (giá trị cực đại)
f(2) = 8 - 12 + 2 = -2 (giá trị cực tiểu)
Mẹo giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm: Quy tắc lũy thừa, quy tắc tích, quy tắc thương, quy tắc chuỗi,...
- Kiểm tra lại kết quả: Đảm bảo rằng bạn đã tính đạo hàm chính xác và giải phương trình đúng.
- Vẽ đồ thị hàm số: Sử dụng đồ thị để kiểm tra kết quả và hiểu rõ hơn về hành vi của hàm số.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng.
Ứng dụng của đạo hàm trong thực tế
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Tính vận tốc, gia tốc, lực,...
- Kinh tế: Tính chi phí biên, doanh thu biên, lợi nhuận biên,...
- Kỹ thuật: Tối ưu hóa thiết kế, điều khiển hệ thống,...
Tài liệu tham khảo thêm
Để hiểu rõ hơn về đạo hàm và ứng dụng của nó, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 tập 1
- Sách bài tập Toán 11 tập 1
- Các trang web học Toán trực tuyến như tusach.vn
Hy vọng bài giải chi tiết này sẽ giúp bạn hiểu rõ hơn về bài 4.25 trang 119 SGK Toán 11 tập 1. Chúc bạn học tốt!
