Giải mục 1 trang 20, 21, 22, 23, 24, 25, 26, 27, 28 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 20-28 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của tusach.vn. Chúng tôi xin giới thiệu bộ giải đáp án chi tiết và dễ hiểu cho các bài tập trong mục 1, trang 20 đến trang 28 của sách giáo khoa Toán 11 tập 1 - Cùng khám phá.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Hàm số (fleft( x right) = {x^2}) có đồ thị như Hình 1.32.
Hoạt động 1
Hàm số \(f\left( x \right) = {x^2}\) có đồ thị như Hình 1.32.
a) So sánh \(f\left( { - 1} \right)\) và \(f\left( 1 \right)\) , \(f\left( { - 2} \right)\)và \(f\left( 2 \right)\), \(f\left( { - x} \right)\) và \(f\left( x \right)\).
b) Đồ thị của hàm số nhận trục nào làm trục đối xứng?
Hàm số \(y = f\left( x \right) = x\), với \(x \in \left[ { - 2;2} \right]\), có đồ thị như Hình 1.33.
a) So sánh \(f\left( { - 1} \right)\) và \(f\left( 1 \right)\) , \(f\left( { - 2} \right)\)và \(f\left( 2 \right)\), \(f\left( { - x} \right)\) và \(f\left( x \right)\) khi \(x \in \left[ { - 2;2} \right]\).
b) Đồ thị của hàm số nhận điểm nào làm tâm đối xứng?

Phương pháp giải:
Thay lần lượt \(x = - 1,1, - 2,2, - x,x\) vào hàm số.
Lời giải chi tiết:
Hình 1.32
a)
\(\begin{array}{l}f\left( { - 1} \right) = 1 = f\left( 1 \right)\\f\left( { - 2} \right) = 4 = f\left( 2 \right)\\f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\end{array}\)
b) Đồ thị của hàm số nhận trục Oy làm trục đối xứng.
Hình 1.33
a)
\(\begin{array}{l}f\left( { - 1} \right) = - 1 = - f\left( 1 \right)\\f\left( { - 2} \right) = - 2 = - f\left( 2 \right)\\f\left( { - x} \right) = - x = - f\left( x \right)\end{array}\)
b) Đồ thị của hàm số nhận điểm \(O\left( {0;0} \right)\) làm tâm đối xứng.
Luyện tập 1
Xác định hàm số chẵn, hàm số lẻ trong các hàm số sau:
a) \(y = f\left( x \right) = 4x - 3;\)
b) \(y = g\left( x \right) = 2{x^2} - 6;\)
c) \(y = h\left( x \right) = {x^3} - 3x.\)
Phương pháp giải:
Thay \( - x\) vào hàm số.
\(f\left( { - x} \right) = f\left( x \right)\) là hàm số chẵn, \(f\left( { - x} \right) = - f\left( x \right)\) là hàm số lẻ.
Lời giải chi tiết:
a)
\(\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow - x \in D\end{array}\)
\(f\left( { - x} \right) = 4\left( { - x} \right) - 3 = - 4x - 3 \ne f\left( x \right) = 4x - 3\)
Vậy hàm số đã cho không phải hàm số chẵn cũng không phải hàm số lẻ.
b)
\(\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow - x \in D\end{array}\)
\(g\left( { - x} \right) = 2{\left( { - x} \right)^2} - 6 = 2{x^2} - 6 = g\left( x \right)\)
Vậy hàm số đã cho là hàm số chẵn.
c)
\(\begin{array}{l}D = \mathbb{R}\\\forall x \in D \Rightarrow - x \in D\end{array}\)
\(h\left( { - x} \right) = {\left( { - x} \right)^3} - 3\left( { - x} \right) = - {x^3} + 3x = - \left( {{x^3} - 3x} \right) = - h\left( x \right)\)
Vậy hàm số đã cho là hàm số lẻ.
Hoạt động 2
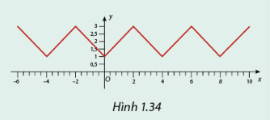
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 1.34.
a) So sánh \(f\left( { - 4} \right),f\left( 0 \right),f\left( 4 \right),f\left( 8 \right).\).
b) Tìm một số \(T \ne 0\) sao cho \(f\left( {x + T} \right) = f\left( x \right)\), với x = -6, x = -2, x = 2, x = 6.
c) Nhận xét đồ thị của hàm số trên các đoạn \(\left[ { - 4;0} \right],\left[ {0;4} \right]\) và \(\left[ {4;8} \right]\).

Phương pháp giải:
a) Tìm tung độ khi hoành độ bằng -4, 0, 4, 8 và so sánh các hoành độ này.
b) Tìm tung độ khi hoành độ bằng -6, -2, 2, 6 và so sánh các hoành độ này. Nhận xét khoảng cách giữa các số -6, -2, 2, 6.
c) Quan sát hình dạng đồ thị trên các đoạn \(\left[ { - 4;0} \right],\left[ {0;4} \right]\) và \(\left[ {4;8} \right]\).
Lời giải chi tiết:
a) \(f\left( { - 4} \right) = f\left( 0 \right) = f\left( 4 \right) = f\left( 8 \right) = 1\)
b) \(f\left( { - 6} \right) = f\left( { - 2} \right) = f\left( 2 \right) = f\left( 6 \right) = 3\)
Vậy T là bội của 4.
c) Đồ thị hàm số trên các đoạn \(\left[ { - 4;0} \right],\left[ {0;4} \right]\) và \(\left[ {4;8} \right]\) giống nhau.
Luyện tập 2
Hàm số hằng \(y = f\left( x \right) = c\) (c là hằng số) có phải là một hàm số tuần hoàn không? Vì sao?
Phương pháp giải:
Hàm hằng là hàm số mà y không thay đổi \(\forall x\).
Lời giải chi tiết:
Hàm hằng là hàm số mà y không thay đổi \(\forall x\) nên hàm hằng là hàm số tuần hoàn.
Giải mục 1 trang 20-28 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Hướng dẫn
Mục 1 của SGK Toán 11 tập 1 - Cùng khám phá tập trung vào các kiến thức cơ bản về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 11.
Nội dung chính của Mục 1
- Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0.
- Tính chất của hàm số bậc hai: Xác định đỉnh, trục đối xứng, khoảng đồng biến, nghịch biến.
- Đồ thị hàm số bậc hai (Parabol): Vẽ parabol, xác định các yếu tố quan trọng như đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến hàm số bậc hai.
Giải chi tiết các bài tập trang 20-28
Dưới đây là giải chi tiết các bài tập từ trang 20 đến trang 28 của SGK Toán 11 tập 1 - Cùng khám phá. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng để giúp các em hiểu sâu sắc hơn về bài toán.
Bài 1 (Trang 20): Xác định hệ số a, b, c của hàm số
Bài tập này yêu cầu các em xác định hệ số a, b, c của hàm số bậc hai cho trước. Để làm được bài này, các em cần nắm vững định nghĩa hàm số bậc hai và biết cách nhận biết các hệ số.
Ví dụ: Cho hàm số y = 2x2 - 3x + 1. Xác định hệ số a, b, c.
Giải: a = 2, b = -3, c = 1.
Bài 2 (Trang 21): Tìm đỉnh của parabol
Bài tập này yêu cầu các em tìm tọa độ đỉnh của parabol. Để làm được bài này, các em cần sử dụng công thức tính tọa độ đỉnh: xđỉnh = -b/2a, yđỉnh = -Δ/4a (với Δ = b2 - 4ac).
Bài 3 (Trang 22-28): Các bài tập ứng dụng
Các bài tập từ trang 22 đến trang 28 thường là các bài tập ứng dụng, yêu cầu các em vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Các bài tập này có thể liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải các phương trình bậc hai.
Lưu ý khi giải bài tập
- Luôn kiểm tra lại kết quả sau khi giải bài tập.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Tham khảo các tài liệu tham khảo khác để hiểu sâu sắc hơn về bài toán.
- Nếu gặp khó khăn, hãy hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.
Kết luận
Hy vọng với bộ giải đáp án chi tiết này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 11. Chúc các em học tốt và đạt kết quả cao trong các kỳ thi sắp tới!
Mọi thắc mắc hoặc cần hỗ trợ thêm, đừng ngần ngại liên hệ với tusach.vn. Chúng tôi luôn sẵn sàng đồng hành cùng các em trên con đường chinh phục tri thức.