Lý thuyết Giới hạn của dãy số - SGK Toán 11 Cùng khám phá
Tổng quan nội dung
Lý thuyết Giới hạn của dãy số - Nền tảng Toán 11
Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của dãy số, một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 11.
Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về khái niệm giới hạn, các định nghĩa, tính chất và ứng dụng của giới hạn dãy số, hoàn toàn dựa trên nội dung SGK Toán 11.
Chúng ta sẽ cùng nhau khám phá cách giải các bài tập liên quan đến giới hạn dãy số một cách hiệu quả và dễ dàng.
I. Giới hạn hữu hạn của dãy số
I. Giới hạn hữu hạn của dãy số
1. Dãy số có giới hạn bằng 0
- Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.
Kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\) khi \(n \to + \infty \) hay \(\lim {u_n} = 0\).
* Chú ý:
+ \(\lim \frac{1}{{{n^k}}} = 0,k \in \mathbb{Z}.\)
+ Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\)
2. Dãy số có giới hạn hữu hạn
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) hay \({u_n} \to a\)khi \(n \to + \infty \).
* Chú ý: Nếu \({u_n} = c\) (c là hằng số) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = c\)
3. Định lí về giới hạn hữu hạn
Cho \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) và c là hằng số thì
- \(\mathop {\lim }\limits_{n \to + \infty } ({u_n} \pm {v_n}) = a \pm b\)
- \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = a.b\)
- \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)\)
- Nếu \({u_n} \ge 0\) thì với mọi n và \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) thì \(a \ge 0\) và \(\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n}} = \sqrt a \)
4. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn là:
\(S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)\)
II. Giới hạn vô cực
- Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( + \infty \)khi \(n \to + \infty \) nếu \({u_n}\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \) hay \({u_n} \to + \infty \) khi \(n \to + \infty \).
- Dãy số \(\left( {{u_n}} \right)\) được gọi là có giới hạn \( - \infty \)khi \(n \to + \infty \) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left( { - {u_n}} \right) = + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = - \infty \) hay \({u_n} \to - \infty \) khi \(n \to + \infty \).
*Nhận xét:
\(\begin{array}{l}a,\lim {n^k} = + \infty ,k \in \mathbb{N},k \ge 1.\\b,\lim {q^n} = + \infty ;q \in \mathbb{R},q > 1.\end{array}\)
* Chú ý:
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a\)và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = + \infty \)(hoặc\(\mathop {\lim }\limits_{x \to + \infty } {v_n} = - \infty \))thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = 0\).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,{v_n} > 0\)thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = + \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,{v_n} < 0\)thì \(\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = - \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a > 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \)thì \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = + \infty \).
Nếu \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a < 0\) và \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty \)thì \(\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = - \infty \)
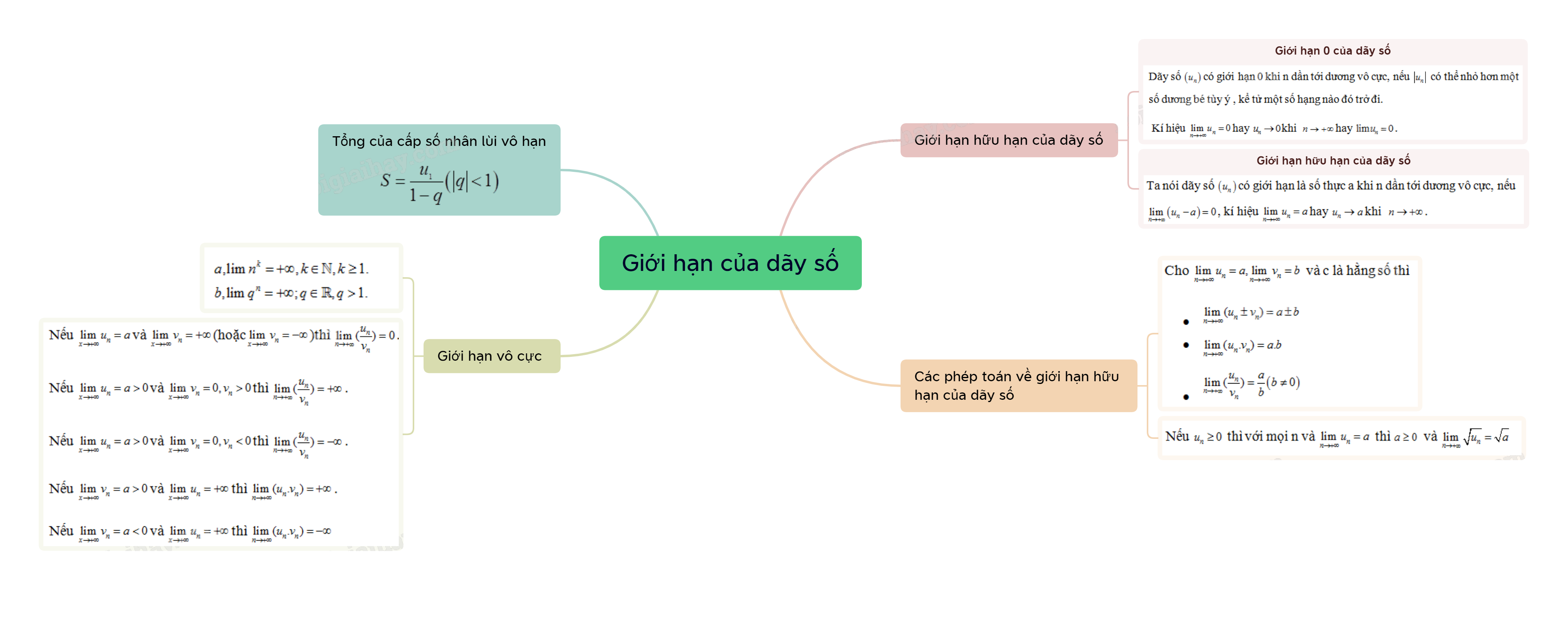
Lý Thuyết Giới Hạn của Dãy Số - SGK Toán 11: Tổng Quan và Ứng Dụng
Giới hạn của dãy số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc xây dựng các khái niệm toán học cao cấp hơn như đạo hàm, tích phân. Trong chương trình Toán 11, việc nắm vững lý thuyết này là điều kiện cần thiết để giải quyết các bài toán liên quan đến dãy số và chuỗi số.
1. Khái Niệm Giới Hạn của Dãy Số
Một dãy số (un) được gọi là có giới hạn hữu hạn L nếu với mọi ε > 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có |un - L| < ε. Ký hiệu: limn→∞ un = L.
Dãy số (un) được gọi là có giới hạn vô cùng dương nếu với mọi M > 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có un > M. Ký hiệu: limn→∞ un = +∞.
Tương tự, dãy số (un) được gọi là có giới hạn âm vô cùng nếu với mọi M < 0, tồn tại một số tự nhiên N sao cho với mọi n > N, ta có un < M. Ký hiệu: limn→∞ un = -∞.
2. Các Tính Chất của Giới Hạn
- Tính duy nhất: Nếu một dãy số có giới hạn thì giới hạn đó là duy nhất.
- Tính chất cộng: limn→∞ (un + vn) = limn→∞ un + limn→∞ vn (với điều kiện các giới hạn tồn tại).
- Tính chất nhân: limn→∞ (un * vn) = limn→∞ un * limn→∞ vn (với điều kiện các giới hạn tồn tại).
- Tính chất chia: limn→∞ (un / vn) = (limn→∞ un) / (limn→∞ vn) (với điều kiện limn→∞ vn ≠ 0).
3. Các Dạng Giới Hạn Đặc Biệt
a) Giới hạn của dãy số không đổi: limn→∞ c = c (với c là một hằng số).
b) Giới hạn của dãy số qn:
- Nếu |q| < 1 thì limn→∞ qn = 0.
- Nếu q = 1 thì limn→∞ qn = 1.
- Nếu q > 1 thì limn→∞ qn = +∞.
- Nếu q ≤ -1 thì dãy số qn không có giới hạn.
4. Bài Tập Ví Dụ và Phương Pháp Giải
Ví dụ 1: Tính limn→∞ (2n + 1) / (n - 3).
Giải:
limn→∞ (2n + 1) / (n - 3) = limn→∞ (2 + 1/n) / (1 - 3/n) = (2 + 0) / (1 - 0) = 2.
Ví dụ 2: Tính limn→∞ (1/2)n.
Giải:
Vì |1/2| < 1 nên limn→∞ (1/2)n = 0.
5. Ứng Dụng của Giới Hạn Dãy Số
Giới hạn dãy số có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
- Tính diện tích hình phẳng.
- Tính đạo hàm và tích phân.
- Giải các bài toán về chuỗi số.
- Mô tả các hiện tượng vật lý và kinh tế.
6. Luyện Tập Thêm
Để nắm vững kiến thức về giới hạn dãy số, bạn nên luyện tập thêm các bài tập trong SGK Toán 11 và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu rõ các định nghĩa, tính chất và phương pháp giải bài tập.
Chúc bạn học tốt!