Giải mục 3 trang 78, 79 SGK Toán 11 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 78, 79 SGK Toán 11 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.

Bài viết này sẽ cung cấp đáp án chính xác, dễ hiểu, cùng với phương pháp giải chi tiết từng bài tập, giúp các em hiểu sâu sắc kiến thức và tự tin hơn trong quá trình học tập.

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Xét hai đường thẳng chéo nhau AA’ và DC’

Hoạt động 6

Cho hình hộp chữ nhật ABCD.A’B’C’D’. Xét hai đường thẳng chéo nhau AA’ và DC’

a) Đường thẳng A'D' có đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C không? Vì sao?

b) Tìm mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng AA’ và song song với D’C. So sánh d(D’C, \(\left( \alpha \right)\)) và A’D’.

Giải mục 3 trang 78, 79 SGK Toán 11 tập 2 - Cùng khám phá 1

Phương pháp giải:

Quan sát hình vẽ.

Lời giải chi tiết:

a) Đường thẳng A'D' không đồng thời cắt và vuông góc với hai đường thẳng AA’ và D’C vì A’D’ không vuông góc với D’C.

b) \(\left( \alpha \right)\) là (AA’B)

d(D’C, (AA’B)) = A’D’.

Luyện tập 6

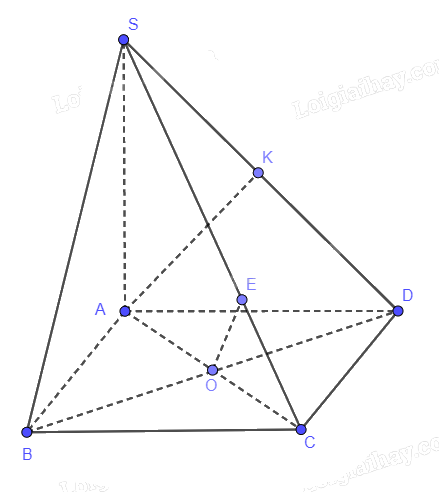
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), SA = 3a; ABCD là hình vuông cạnh a, O là giao điểm của AC và BD. Tính khoảng cách giữa:

a) BD và SC

b) AB và SC.

Phương pháp giải:

a) Tìm khoảng cách giữa a và b:

+ Tìm (P) chứa a và vuông góc với b.

+ Tìm giao điểm H thỏa mãn thuộc b và nằm trong (P).

+ Tại (P), dựng HK vuông góc với a tại K.

+ HK là khoảng cách cần tìm.

b) Tìm khoảng cách giữa a và b:

+ Tìm (P) chứa a và song song với b.

+ \(d\left( {a,b} \right) = d\left( {b,\left( P \right)} \right)\).

Lời giải chi tiết:

Giải mục 3 trang 78, 79 SGK Toán 11 tập 2 - Cùng khám phá 1

a) BD vuông góc với (SAC)

Kẻ OE vuông góc với SC

Vậy OE là khoảng cách cần tìm

\(\begin{array}{l}\frac{1}{{O{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{2{a^2}}}\\ \Rightarrow OE = \frac{{3\sqrt {22} }}{{11}}a\end{array}\)

b) Kẻ AK vuông góc với SD

Ta có: AB // CD nên AB // (SCD)

\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right) = AK\)

\(\begin{array}{l}AK.SD = SA.AD\\ \Leftrightarrow AK = \frac{{3a.a}}{{\sqrt {{{\left( {3a} \right)}^2} + {a^2}} }} = \frac{{3\sqrt {10} }}{{10}}a\end{array}\)

Giải mục 3 trang 78, 79 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải

Mục 3 trang 78, 79 SGK Toán 11 tập 2 tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức về:

Định nghĩa và tính chất của các hàm số lượng giác (sin, cos, tan, cot).
Biểu diễn hình học của hàm số lượng giác.
Phương trình lượng giác cơ bản và phương pháp giải.
Ứng dụng của hàm số lượng giác trong việc giải quyết các bài toán thực tế.

Nội dung chi tiết lời giải các bài tập

Bài 1: (Trang 78 SGK Toán 11 tập 2)

Bài 1 yêu cầu học sinh chứng minh một đẳng thức lượng giác. Để giải bài này, các em cần nắm vững các công thức lượng giác cơ bản và sử dụng phương pháp biến đổi tương đương.

Lời giải: (Giải chi tiết bài 1 với các bước biến đổi rõ ràng)

Bài 2: (Trang 78 SGK Toán 11 tập 2)

Bài 2 là một bài tập về giải phương trình lượng giác. Các em cần xác định đúng phương pháp giải phù hợp với từng loại phương trình (phương trình lượng giác cơ bản, phương trình lượng giác đưa về phương trình bậc hai,...).

Lời giải: (Giải chi tiết bài 2 với các bước giải rõ ràng)

Bài 3: (Trang 79 SGK Toán 11 tập 2)

Bài 3 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số lượng giác. Để giải bài này, các em cần phân tích đề bài, xây dựng mô hình toán học và sử dụng các kiến thức về hàm số lượng giác để tìm ra lời giải.

Lời giải: (Giải chi tiết bài 3 với các bước giải rõ ràng)

Mẹo giải nhanh và hiệu quả

Để giải các bài tập về hàm số lượng giác một cách nhanh chóng và hiệu quả, các em có thể tham khảo một số mẹo sau:

Nắm vững các công thức lượng giác cơ bản và các công thức biến đổi.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính bỏ túi để kiểm tra lại kết quả.
Tham khảo các tài liệu tham khảo và các bài giải trên mạng.

Bài tập tương tự

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể thử sức với một số bài tập tương tự sau:

Giải phương trình: sin(x) = 1/2
Chứng minh đẳng thức: cos²(x) + sin²(x) = 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 2sin(x) + 1

Kết luận

Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 3 trang 78, 79 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao!

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!

Giải mục 3 trang 78, 79 SGK Toán 11 tập 2 - Cùng khám phá