Lý Thuyết Dãy Số - SGK Toán 11 | tusach.vn

Lý thuyết Dãy số - SGK Toán 11 Cùng khám phá

Lý thuyết Dãy số - SGK Toán 11: Nền tảng vững chắc cho môn Toán

Dãy số là một trong những khái niệm cơ bản và quan trọng trong chương trình Toán học lớp 11. Việc nắm vững lý thuyết dãy số không chỉ giúp học sinh giải quyết các bài tập trong SGK mà còn là nền tảng cho việc học các kiến thức nâng cao hơn trong các lớp học tiếp theo.

Tại tusach.vn, chúng tôi cung cấp tài liệu học tập đầy đủ và chi tiết về lý thuyết dãy số, giúp bạn hiểu rõ các khái niệm, định lý và phương pháp giải bài tập một cách hiệu quả.

1. Dãy số

1. Dãy số

Dãy số vô hạn

- Một hàm số\(u = u\left( n \right)\) xác định trên tập các số nguyên dương \({\mathbb{N}^*}\) được gọi là một dãy số vô hạn (gọi tắt là dãy số).

Kí hiệu là \(u\left( n \right) = {u_n}\) hay dãy số \(\left( {{u_n}} \right)\).

- Một hàm số \(u = u\left( n \right)\) xác định trên tập \(M = \left\{ {1;2;3;...;m} \right\},m \in {\mathbb{N}^*}\) được gọi là một dãy số hữu hạn.

*Nhận xét:

- Dãy số \(\left( {{u_n}} \right)\) được viết dưới dạng khai triển \({u_1},{u_2},{u_3},...,{u_n},...\) Số \({u_1}\) là số hạng đầu; \({u_n}\) là số hạng thứ n và gọi là số hạng tổng quát của dãy số; n được gọi là chỉ số.

- Dạng khai triển của dãy số hữu hạn là \({u_1},{u_2},{u_3},...,{u_m}\). Trong đó, số \({u_1}\) gọi là số hạng đầu, \({u_m}\) là số hạng cuối.

II. Cách cho một dãy số

Một dãy số có thể cho bằng:

Liệt kê các số hạng (với các dãy hữu hạn).
Công thức của số hạng tổng quát \({u_n}\).
Phương pháp truy hồi:

- Cho số hạng thứ nhất \({u_1}\) (hoặc một vài số hạng đầu tiên)

- Cho một công thức tính \({u_n}\) theo\({u_{n - 1}}\) (hoặc theo vài số hạng đứng ngay trước nó).

Phương pháp mô tả.

III. Dãy số tăng, dãy số giảm và dãy số bị chặn

1. Dãy số tăng, dãy số giảm

Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có \({u_{n + 1}} > {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có \({u_{n + 1}} < {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).

2. Dãy số bị chặn

Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu \(\exists \) số M sao cho \({u_n} \le M,\) \(\forall n \in {\mathbb{N}^*}\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu \(\exists \) số m sao cho \({u_n} \ge m,\) \(\forall n \in {\mathbb{N}^*}\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho \(m \le {u_n} \le M,\)\(\forall n \in {\mathbb{N}^*}\).

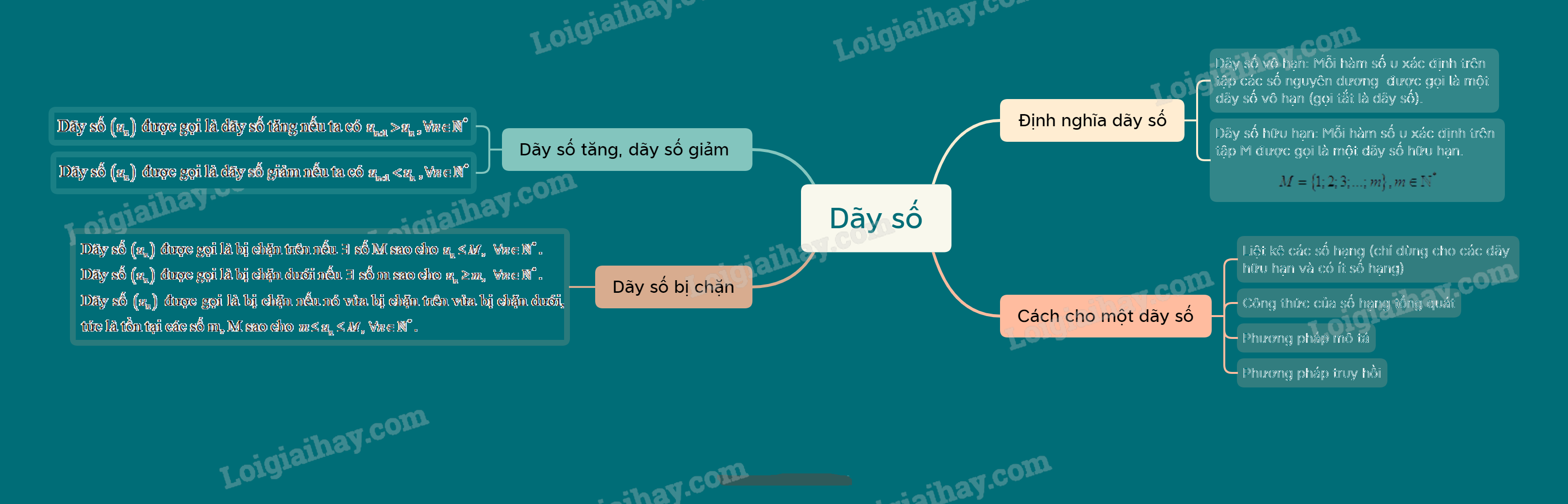
Lý thuyết Dãy số - SGK Toán 11 Cùng khám phá 1

Lý Thuyết Dãy Số - SGK Toán 11: Tổng Quan và Các Khái Niệm Quan Trọng

Dãy số là một hàm số được xác định trên tập hợp các số tự nhiên hoặc một tập con của nó. Nói cách khác, dãy số là một tập hợp các số được sắp xếp theo một thứ tự nhất định. Trong chương trình Toán 11, học sinh sẽ được làm quen với các loại dãy số cơ bản như dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm, và đặc biệt là các dãy số đặc biệt như cấp số cộng và cấp số nhân.

1. Các Khái Niệm Cơ Bản về Dãy Số

Số hạng của dãy số: Mỗi phần tử trong dãy số được gọi là một số hạng.
Dãy số hữu hạn: Dãy số có số lượng số hạng là hữu hạn. Ví dụ: 1, 2, 3, 4, 5.
Dãy số vô hạn: Dãy số có số lượng số hạng là vô hạn. Ví dụ: 1, 2, 3, 4, ...
Dãy số tăng: Dãy số mà mỗi số hạng lớn hơn số hạng đứng trước nó.
Dãy số giảm: Dãy số mà mỗi số hạng nhỏ hơn số hạng đứng trước nó.

2. Cấp Số Cộng

Cấp số cộng là một dãy số mà mỗi số hạng sau được tạo thành bằng cách cộng một số không đổi (công sai) vào số hạng đứng trước nó. Công thức tổng quát của cấp số cộng là: u_n = u₁ + (n - 1)d, trong đó:

u_n là số hạng thứ n
u₁ là số hạng đầu tiên
d là công sai

Tổng của n số hạng đầu tiên của cấp số cộng được tính bằng công thức: S_n = n/2 * (u₁ + u_n) hoặc S_n = n/2 * [2u₁ + (n - 1)d]

3. Cấp Số Nhân

Cấp số nhân là một dãy số mà mỗi số hạng sau được tạo thành bằng cách nhân số hạng đứng trước nó với một số không đổi (tỷ số). Công thức tổng quát của cấp số nhân là: u_n = u₁ * q^{(n - 1)}, trong đó:

u_n là số hạng thứ n
u₁ là số hạng đầu tiên
q là tỷ số

Tổng của n số hạng đầu tiên của cấp số nhân được tính bằng công thức:

Nếu q ≠ 1: S_n = u₁ * (1 - qⁿ) / (1 - q)
Nếu q = 1: S_n = n * u₁

4. Giới Hạn của Dãy Số

Khái niệm giới hạn của dãy số là một khái niệm quan trọng trong giải tích. Một dãy số được gọi là có giới hạn nếu nó tiến tới một giá trị xác định khi n tiến tới vô cùng. Việc tìm giới hạn của dãy số giúp chúng ta hiểu rõ hơn về hành vi của dãy số khi số lượng số hạng tăng lên.

5. Ứng Dụng của Lý Thuyết Dãy Số

Lý thuyết dãy số có nhiều ứng dụng trong thực tế, chẳng hạn như:

Tính lãi kép: Công thức tính lãi kép dựa trên cấp số nhân.
Mô hình tăng trưởng dân số: Dãy số có thể được sử dụng để mô hình hóa sự tăng trưởng dân số.
Phân tích chuỗi thời gian: Dãy số được sử dụng để phân tích các chuỗi thời gian trong kinh tế và tài chính.

Bài Tập Vận Dụng

Để củng cố kiến thức về lý thuyết dãy số, bạn có thể thực hành giải các bài tập sau:

Tìm số hạng thứ 10 của cấp số cộng có số hạng đầu tiên là 2 và công sai là 3.
Tìm tổng của 20 số hạng đầu tiên của cấp số nhân có số hạng đầu tiên là 1 và tỷ số là 2.
Tính giới hạn của dãy số u_n = 1/n khi n tiến tới vô cùng.

Kết Luận

Lý thuyết dãy số là một phần quan trọng của chương trình Toán 11. Việc nắm vững các khái niệm và công thức liên quan đến dãy số sẽ giúp bạn giải quyết các bài tập một cách hiệu quả và ứng dụng kiến thức vào thực tế. Hãy luyện tập thường xuyên và tìm kiếm sự hỗ trợ từ giáo viên hoặc các nguồn tài liệu học tập uy tín để đạt được kết quả tốt nhất.