Bài 8.25 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.25 trang 79 SGK Toán 11 tập 2
Bài 8.25 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán liên quan đến đạo hàm của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình lăng trụ tam giác ABC.A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B, C và AA’ = AB = 2a
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B, C và AA’ = AB = 2a. Tính khoảng cách giữa hai đáy của hình lăng trụ.
Phương pháp giải - Xem chi tiết
Khoảng cách giữa 2 mặt phẳng song song là khoảng cách từ 1 điểm bất kì của mặt này đến mặt phẳng kia.
Lời giải chi tiết
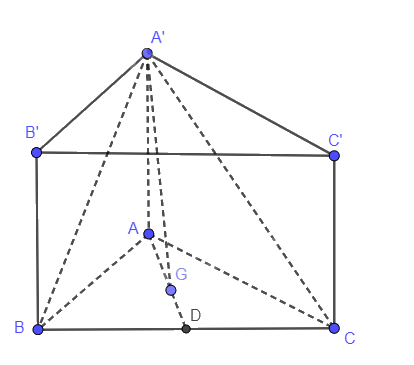
Gọi D là trung điểm BC, G là trọng tâm tam giác ABC
\(\begin{array}{l}AD = \sqrt 2 a\\ \Rightarrow AG = \frac{{2\sqrt 2 }}{3}a\end{array}\)
A’G vuông góc với (ABC) nên A’G vuông góc với AG
\(\begin{array}{l}A'G = \sqrt {AA{'^2} - A{G^2}} = \sqrt {4{a^2} - {{\left( {\frac{{2\sqrt 2 }}{3}a} \right)}^2}} = \frac{{2\sqrt 7 }}{3}a\\\end{array}\)
Bài 8.25 Trang 79 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích
Bài 8.25 trang 79 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phân tích bài tập này:
Nội dung bài tập:
(Giả sử nội dung bài tập là: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
Lời giải:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính đạo hàm bậc nhất f'(x).
- Bước 3: Tìm các điểm dừng (điểm mà f'(x) = 0 hoặc không xác định).
- Bước 4: Lập bảng biến thiên để xác định các điểm cực trị.
- Bước 5: Kết luận.
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Hàm số y = f(x) = x3 - 3x2 + 2 có tập xác định là D = ℝ (tập hợp tất cả các số thực).
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Dựa vào bảng biến thiên, ta thấy:
Phân tích và mở rộng:
Bài tập này yêu cầu học sinh nắm vững các bước tìm cực trị của hàm số: tìm tập xác định, tính đạo hàm bậc nhất, tìm điểm dừng, lập bảng biến thiên và kết luận. Việc hiểu rõ các bước này sẽ giúp học sinh giải quyết các bài toán tương tự một cách hiệu quả.
Ngoài ra, học sinh cần chú ý đến việc kiểm tra điều kiện cần và điều kiện đủ để xác định các điểm cực trị. Điều kiện cần là đạo hàm bậc nhất bằng 0 hoặc không xác định, còn điều kiện đủ là đạo hàm bậc nhất đổi dấu khi đi qua điểm dừng.
Bài tập tương tự:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự trong SGK và sách bài tập Toán 11 tập 2. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải toán.
Lưu ý: Đây chỉ là một ví dụ về lời giải và phân tích bài 8.25 trang 79 SGK Toán 11 tập 2. Nội dung cụ thể của bài tập có thể khác nhau tùy thuộc vào phiên bản SGK.
Chúc các em học tốt!
Truy cập tusach.vn để xem thêm nhiều bài giải Toán 11 và các môn học khác.