Giải mục 2 trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
a) Trên một đường tròn, cung nửa đường tròn có số đo bằng bao nhiêu radian? Góc ở tâm chắn cung nửa đường tròn có số đo bằng bao nhiêu radian? b) Từ đó tìm mối liên hệ giữa đơn vị độ và đơn vị radian.
Hoạt động 2
a) Trên một đường tròn, cung nửa đường tròn có số đo bằng bao nhiêu radian? Góc ở tâm chắn cung nửa đường tròn có số đo bằng bao nhiêu radian?
b) Từ đó tìm mối liên hệ giữa đơn vị độ và đơn vị radian.
Phương pháp giải:
- Theo lý thuyết, cung có độ dài bằng r (bán kính) là cung có số đo 1 rad.
\( \Rightarrow \) Cung có độ dài \(l\) thì có số đo là \(\frac{l}{r}\) rad.
- Cung nửa đường tròn có độ dài là \(\pi r\).
- Theo lý thuyết, góc ở tâm chắn cung có số đo 1 rad là góc có số đo 1 rad.
\( \Rightarrow \)Góc ở tâm chắn cung có số đo \(\alpha \) rad là góc có số đo \(\alpha \) rad.
Lời giải chi tiết:
a) Nửa đường tròn có độ dài là \(\pi r\)\( \Rightarrow \) Cung nửa đường tròn có số đo là \(\frac{{\pi r}}{r} = \pi \) rad.
Do đó góc ở tâm chắn nửa đường tròn có số đo là \(\pi \) rad.
b) Nửa đường tròn có số đo là \(\pi \) rad
Mà số đo nửa đường tròn còn bằng 1800
\( \Rightarrow \)\({180^0} = \pi \) rad
\( \Rightarrow {1^0} = \frac{\pi }{{180}}\) rad; 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^0}\).
Luyện tập 1
Đổi 5 rad và \(\frac{\pi }{8}\) rad ra độ.
Phương pháp giải:
Áp dụng công thức: \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
Lời giải chi tiết:
5 rad = \({\left( {5.\frac{{180}}{\pi }} \right)^0} = {\left( {\frac{{900}}{\pi }} \right)^0}\)
\(\frac{\pi }{8}\) rad = \({\left( {\frac{\pi }{8}.\frac{{180}}{\pi }} \right)^0} = 22,{5^0}\)
Hoạt động 3
Trên đường tròn bán kính r, hãy tính:
a) Độ dài của cung nửa đường tròn;
b) Độ dài của cung có số đo \(\alpha \) rad.
Phương pháp giải:
Công thức tính độ dài cung là: \(l = \frac{{\pi Rn}}{{180}}\), trong đó \({n^0}\) là số đo cung cần tìm.
Áp dụng công thức: \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
Lời giải chi tiết:
a) Cung nửa đường tròn có số đo là 1800
Độ dài của cung nửa đường tròn là \(l = \frac{{\pi r180}}{{180}} = \pi r\).
b) \(\alpha \)rad = \({\left( {\alpha .\frac{{180}}{\pi }} \right)^0}\)
\(l = \frac{{\pi r}}{{180}}.\frac{{180\alpha }}{\pi } = \alpha r\).
Vận dụng
Một bức tường của một ngôi nhà có dạng như Hình 1.7, trong đó cung AB là một cung của đường tròn tâm C, bán kính AC. Tính chu vi của bức tường.
Phương pháp giải:
- Chu vi bức tường gồm phần độ dài cung , AH, BK và HK.
- Áp dụng công thức: Trên đường tròn có bán kính \(r\), cung có số đo \(\alpha \) rad có độ dài \(l = \alpha r\).
- Định lý Py – ta – go cho tam giác vuông: Bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
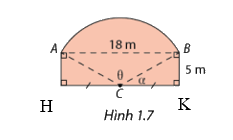
Gọi điểm H, K như trên hình
AB = 18m \( \Rightarrow \)HK = 18m \( \Rightarrow \)CK = 9m
\(\Rightarrow BC = \sqrt {B{K^2} + C{K^2}} = \sqrt {{5^2} + {9^2}} = \sqrt {106} \Rightarrow r = \sqrt {106} \) (m)
Ta có: \(\tan \alpha = \frac{{BK}}{{CK}} = \frac{5}{9}\) \( \Rightarrow \alpha \approx 0,507 rad\)
\(\theta = \pi - 2\alpha = \pi - 2.0,507 \approx 2,128 rad\)
\( \Rightarrow \) Cung AB có độ dài là: \(l = \theta r = 2,128.\sqrt {106} \approx 21,91\)(m)
Vậy chu vi bức tường là: 21,91+5+5+18=49,91 (m)
Hoạt động 4
Hãy xác định số đo của mỗi cung lượng giác (A đến B) khi điểm M di động trên đường tròn từ A đến B trong Hình 1.1.

Phương pháp giải:
- Khi điểm M di động trên đường tròn theo chiều dương từ A đến B tạo nên cung \(\frac{1}{4}\) đường tròn nên có số đo là \(\frac{\pi }{2}\). M đi tiếp mỗi vòng thì thêm \(2\pi \).
- Khi điểm M di động trên đường tròn theo chiều âm từ A đến B tạo nên cung \(\frac{3}{4}\) đường tròn nên có số đo là \( - \frac{{3\pi }}{2}\).
Lời giải chi tiết:
a) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2}\).
b) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2\pi = \frac{{5\pi }}{2}\).
c) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2.2\pi = \frac{{9\pi }}{2}\).
d) Cung lượng giác AB (A đến B) có số đo là \( - \frac{{3\pi }}{2}\).
Luyện tập 2
Tính số đo của mỗi góc lượng giác (OA, OB) trong Hình 1.1.

Phương pháp giải:
Theo lý thuyết, số đo của góc lượng giác (OA, OB)là số đo cung lượng giác (A đến B). Kí hiệu: sđ(OA, OB).
Lời giải chi tiết:
a) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2}\). Vậy sđ(OA, OB) =\(\frac{\pi }{2}\).
b) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2\pi = \frac{{5\pi }}{2}\). Vậy sđ(OA,OB) = \(\frac{{5\pi }}{2}\).
c) Cung lượng giác AB (A đến B) có số đo là \(\frac{\pi }{2} + 2.2\pi = \frac{{9\pi }}{2}\). Vậy sđ(OA,OB) = \(\frac{{9\pi }}{2}\).
d) Cung lượng giác AB (A đến B) có số đo là \( - \frac{{3\pi }}{2}\). Vậy sđ(OA,OB) = \( - \frac{{3\pi }}{2}\).
Hoạt động 5
Giả sử sđ(OA, OB) = \(\frac{\pi }{3}\) và sđ(OB, OC) = \(\frac{\pi }{4}\)(Hình 1.11). Xác định sđ(OA, OC).

Phương pháp giải:
Áp dụng hệ thức Chasles: sđ(OA, OB) + sđ(OB, OC) = sđ(OA, OC) + \(k2\pi \), \(k \in \mathbb{Z}\).
Lời giải chi tiết:
Áp dụng hệ thức Chasles: sđ(OA, OB) + sđ(OB, OC) = sđ(OA, OC) + \(k2\pi \), \(k \in \mathbb{Z}\)
\( \Leftrightarrow \frac{\pi }{4} + \frac{\pi }{3} = \frac{{7\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\).
Luyện tập 3
Nếu góc lượng giác (OA, OB) và (OA, OC) lần lượt có số đo là \( - \frac{{7\pi }}{4}\) và \(\frac{{13\pi }}{4}\) thì góc lượng giác (OB, OC) có số đo bằng bao nhiêu, biết rằng \(4\pi < \left( {OB,OC} \right) < 6\pi \)?
Phương pháp giải:
Áp dụng hệ quả của hệ thức Chasles: sđ(OB, OC) = sđ(OA, OC) - sđ(OA, OB) + \(k2\pi \), \(k \in \mathbb{Z}\).
Lời giải chi tiết:
Áp dụng công thức: sđ(OB, OC) = sđ(OA, OC) - sđ(OA, OB) + \(k2\pi \), \(k \in \mathbb{Z}\)
\( \Leftrightarrow - \frac{{7\pi }}{4} - \frac{{13\pi }}{4} + k2\pi = - 5\pi + k2\pi ,k \in \mathbb{Z}\)
Mà \(4\pi < \left( {OB,OC} \right) < 6\pi \)
\(\begin{array}{l} \Rightarrow 4\pi < - 5\pi + k2\pi < 6\pi \\ \Leftrightarrow 9\pi < k2\pi < 11\pi \\ \Leftrightarrow 4,5 < k < 5,5\\ \Rightarrow k = 5\end{array}\)
Vậy sđ(OB, OC) = \( - 5\pi + 5.2\pi = 5\pi \)
Hoạt động 6
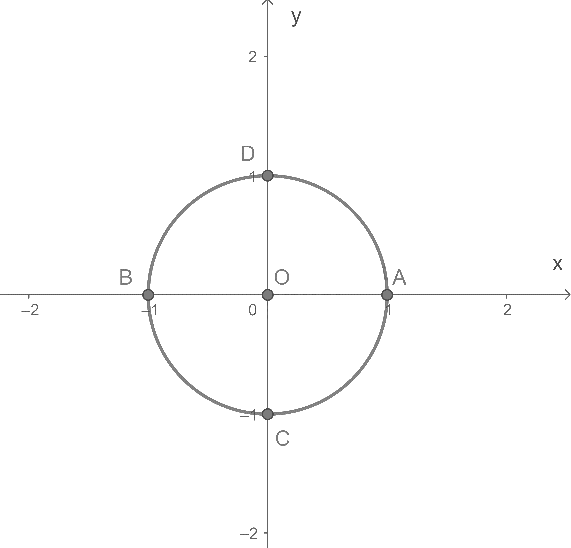
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính R = 1 và tìm giao điểm của nó với các trục tọa độ.
Phương pháp giải:
Vẽ hình và quan sát
Lời giải chi tiết:

Đường tròn tâm O cắt trục Ox tại điểm A(1;0) và B(-1;0), cắt Oy tại điểm C(0;-1) và D(0;1).
Luyện tập 4
Trên đường tròn lượng giác, tìm điểm biểu diễn của các góc lượng giác có số đo sau:
a) \(\frac{{19\pi }}{3}\)
b) \( - {1125^0}\)
Phương pháp giải:
- Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
- Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \) là điểm M trên đường tròn lượng giác sao cho sđ(OA, OM) = \(\alpha \).
Lời giải chi tiết:
a) \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \)
Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{3}\) là điểm C(0;-1).
b) \( - {1125^0} = - {45^0} - {3.360^0}\)
Vậy điểm biểu diễn của góc lượng giác có số đo \( - {1125^0}\) là điểm chính giữa B của cung nhỏ .
Giải mục 2 trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về giới hạn của hàm số. Đây là một phần kiến thức nền tảng quan trọng, giúp học sinh hiểu rõ hơn về sự biến đổi của hàm số khi x tiến tới một giá trị nhất định. Việc nắm vững kiến thức này sẽ là bước đệm quan trọng cho các chương trình học nâng cao hơn.
Nội dung chính của Mục 2 SGK Toán 11 tập 1
- Khái niệm giới hạn của hàm số tại một điểm: Học sinh sẽ được làm quen với khái niệm giới hạn, hiểu ý nghĩa của việc hàm số tiến tới một giá trị khi x tiến tới một điểm cụ thể.
- Các tính chất của giới hạn: Tìm hiểu các tính chất cơ bản của giới hạn, như giới hạn của tổng, hiệu, tích, thương và lũy thừa.
- Các dạng giới hạn cơ bản: Luyện tập giải các bài toán giới hạn đơn giản, sử dụng các công thức và tính chất đã học.
- Ứng dụng của giới hạn: Tìm hiểu cách ứng dụng kiến thức về giới hạn để giải quyết các bài toán thực tế.
Giải chi tiết các bài tập trang 3, 4, 5, 6, 7
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2, trang 3, 4, 5, 6, 7 SGK Toán 11 tập 1:
Bài 1 (Trang 3): Tính các giới hạn sau...
Lời giải: Để tính giới hạn này, ta có thể sử dụng phương pháp chia cả tử và mẫu cho x. Sau khi thực hiện phép chia, ta sẽ thu được kết quả là...
Bài 2 (Trang 4): Tìm giới hạn của hàm số f(x) = ... khi x tiến tới 2.
Lời giải: Trong trường hợp này, ta có thể áp dụng định nghĩa giới hạn để chứng minh giới hạn của hàm số là...
Bài 3 (Trang 5): Cho hàm số f(x) = ... Tính f(1), f(2), f(3).
Lời giải: Để tính các giá trị của hàm số, ta chỉ cần thay x bằng các giá trị tương ứng (1, 2, 3) vào biểu thức của hàm số.
Bài 4 (Trang 6): Chứng minh rằng...
Lời giải: Để chứng minh đẳng thức này, ta cần sử dụng các tính chất của giới hạn và biến đổi biểu thức một cách hợp lý.
Bài 5 (Trang 7): Giải phương trình...
Lời giải: Để giải phương trình này, ta cần tìm các giá trị của x sao cho phương trình được thỏa mãn. Ta có thể sử dụng các phương pháp đại số để giải phương trình.
Mẹo học tập hiệu quả
Để học tốt môn Toán 11, đặc biệt là phần giới hạn, các em cần:
- Nắm vững định nghĩa và các tính chất của giới hạn.
- Luyện tập giải nhiều bài tập khác nhau.
- Hiểu rõ bản chất của bài toán, không học thuộc lòng công thức.
- Sử dụng các công cụ hỗ trợ học tập, như máy tính bỏ túi hoặc phần mềm giải toán.
Tusach.vn - Đồng hành cùng bạn trên con đường chinh phục kiến thức
Tusach.vn cam kết cung cấp cho các em những lời giải chính xác, dễ hiểu và đầy đủ nhất. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác. Chúc các em học tập tốt!