A. Lý thuyết
1. Biến cố hợp và biến cố giao
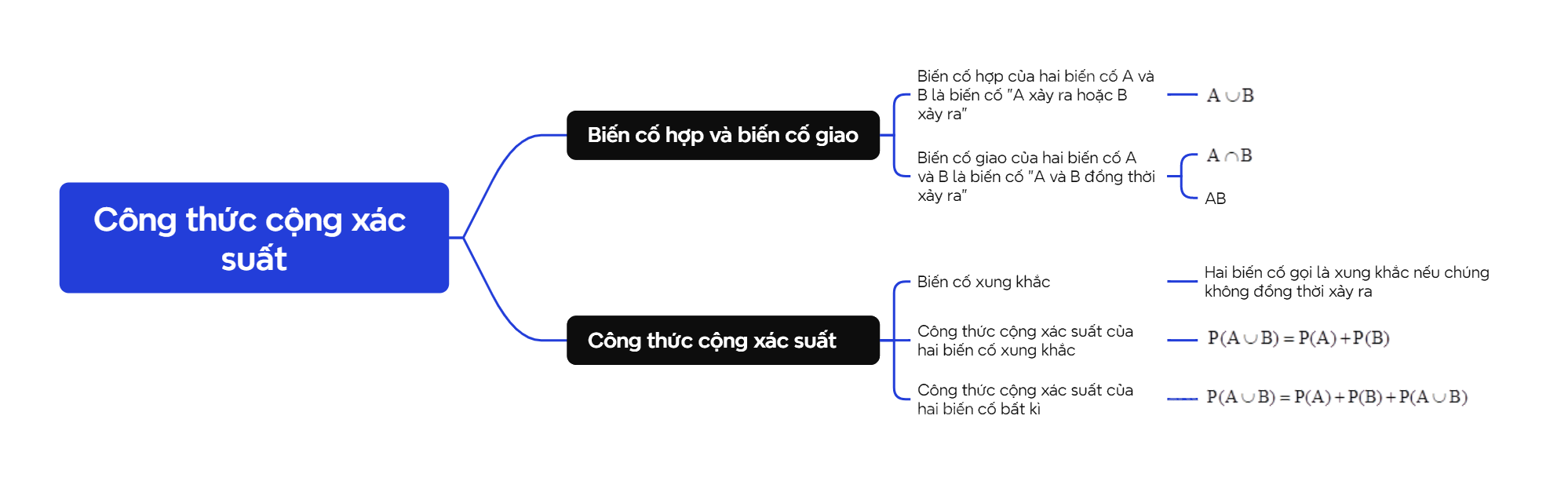
Biến cố hợp của hai biến cố A và B là biến cố "A xảy ra hoặc B xảy ra", ký hiệu \(A \cup B\). Biến cố giao của hai biến cố A và B là biến cố "A và B đồng thời xảy ra", ký hiệu \(A \cap B\) hoặc AB. |
Lưu ý:
- Nếu mô tả các biến cố qua các tập con của không gian mẫu sẽ tạo thuận lợi cho việc tìm các biến cố hợp và giao.
- Trong toàn bộ chương này, ta xét các phép thử mà không gian mẫu có hữu hạn phần tử và đồng khả năng.
2. Công thức cộng xác suất
a) Biến cố xung khắc
| Hai biến cố gọi là xung khắc nếu chúng không đồng thời xảy ra. |
Lưu ý:
- Nếu A và B xung khắc thì \(A \cap B\) là biến cố không thể, nghĩa là \(A \cap B = \emptyset \).
- Hai biến cố đối nhau thì xung khắc. Điều ngược lại là không đúng.
b) Công thức cộng xác suất của hai biến cố xung khắc
Nếu A và B là hai biến cố xung khắc bất kì liên quan đến một phép thử thì \(P(A \cup B) = P(A) + P(B)\). |
Lưu ý: Nếu \(\overline A \) là biến cố đối của A thì A, \(\overline A \) là hai biến cố xung khắc và \(A \cup \overline A = \Omega \). Theo công thức cộng xác suất, ta có:
\(1 = P(\Omega ) = P(A \cup \overline A ) = P(A) + P(\overline A )\).
Do đó \(P(\overline A ) = 1 - P(A)\).
Vậy công thức tính xác suất biến cố đối là trường hợp đặc biệt của công thức cộng hai biến cố xung khắc.
c) Công thức cộng xác suất
Nếu A và B là hai biến cố bất kì liên quan đến một phép thử thì \(P(A \cup B) = P(A) + P(B) + P(A \cup B)\). |
B. Bài tập
Bài 1: Chọn ngẫu nhiên lần lượt hai nhân viên của một công ty và ghi lại giới tính của họ. Xét các biến cố:
A: "Giới tính của một trong hai nhân viên là nam".
B: "Giới tính của hai nhân viên là khác nhau".
C: "Giới tính của hai nhân viên là giống nhau”.
Xác định các biến cố hợp và biến cố giao của:
a) A và B.
b) A và C.
Giải:
Kí hiệu giới tính nữ là F, giới tính nam là M. Không gian mẫu Ω và các biến cố A, B và C được cho bởi:
Ω = {(F;F); (F;M); (M;F); (M;M)}.
A = {(F;M); (M;F)}.
B = {(M;M); (M;F); (F;M)}.
C = {(M;M); (F;F)}.
a) \(A \cup B = A\); \(A \cap B = B\).
b) \(A \cup C = \Omega \); \(A \cap C = \{ (M;M)\} \).
Bài 2: Xét phép thử gieo một đồng xu hai lần và các biến cố sau:
A: "Kết quả gieo hai lần như nhau".
B: "Có ít nhất một lần xuất hiện mặt sấp".
C: "Lần thứ hai mới xuất hiện mặt sấp".
D: "Lần đầu xuất hiện mặt sấp".
Hãy chỉ ra các cặp biến cố xung khắc trong các biến cố đã cho.
Giải:
Ta có A = {SS; NN}; B = {SN; NS; SS}; C = {NS}; D = {SS; SN}.
Do \(A \cap C = \emptyset \) và \(C \cap D = \emptyset \) nên các cặp biến cố xung khắc là A và C, C và D. Ngoài ra, trong các biến cố đã cho không có cặp biến cố xung khắc nào khác.
Bài 3: Một lọ có chứa 1 viên bi đỏ, 3 viên bi xanh lá cây, 4 viên bi đen và 2 viên bi vàng. Lấy ngẫu nhiên 1 viên bi từ trong lọ. Tính xác suất để viên bi lấy được không phải màu đỏ và không phải màu đen.
Giải:
Gọi X là biến cố "viên bi lấy được không phải màu đỏ và không phải màu đen". Biến cố X xảy ra khi viên bi lấy được có màu xanh lá cây hoặc có màu vàng.
Gọi A, B lần lượt là các biến cố "viên bi lấy được có màu xanh lá cây" và "viên bi lấy được có màu vàng". Khi đó, \(X = A \cup B\) và n(A) = 3, n(B) = 2. Hơn nữa, tổng số viên bi trong lọ là:
\(n(\Omega ) = 1 + 3 + 4 + 2 = 10\).
Do A, B là các biến cố xung khắc nên:
\(P(A \cup B) = P(A) + P(B) = \frac{{n(A)}}{{n(\Omega )}} + \frac{{n(B)}}{{n(\Omega )}} = \frac{3}{{10}} + \frac{2}{{10}} = 0,5\).
Vậy \(P(X) = P(A \cup B) = 0,5\).
Bài 4: Trong một buổi tiệc, có:
- 5 người đàn ông có số tuổi không nhỏ hơn 21.
- 4 người đàn ông có số tuổi nhỏ hơn 21.
- 6 người phụ nữ có số tuổi không nhỏ hơn 21.
- 3 người phụ nữ có số tuổi nhỏ hơn 21.
Nếu chọn ngẫu nhiên một người trong buổi tiệc để trao quà thì xác suất để người đó là phụ nữ hoặc có số tuổi nhỏ hơn 21 là bao nhiêu?
Giải:
Tổng số người trong buổi tiệc là n(Ω) = 5 + 4 + 6 + 3 = 18.
Gọi A là biến cố "người được chọn có số tuổi nhỏ hơn 21" và B là biến cố "người được chọn là phụ nữ". Khi đó \(A \cap B\) là biến cố "người được chọn có số tuổi nhỏ hơn 21 và là phụ nữ", còn \(A \cup B\) là biến cố "người được chọn có số tuổi nhỏ hơn 21 hoặc là phụ nữ". Theo định nghĩa trên, ta có:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{3 + 4}}{{18}} = \frac{7}{{18}}\); \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{3 + 6}}{{18}} = \frac{1}{2}\); \(P(A \cap B) = \frac{{n(A \cap B)}}{{n(\Omega )}} = \frac{3}{{18}} = \frac{1}{6}\).
Theo công thức cộng xác suất, ta có \(P(A \cup B) = \frac{7}{{18}} + \frac{9}{{18}} - \frac{3}{{18}} = \frac{{13}}{{18}}\).
