Giải mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài toán.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, logic.
a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \). b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).
Hoạt động 3
a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \).
b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).
Phương pháp giải:
Lời giải chi tiết:
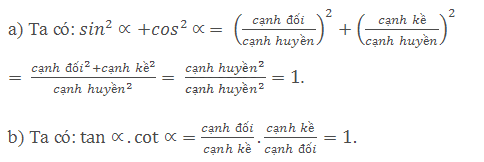
Luyện tập 4
Cường độ ánh sáng I đi xuyên qua một màn lọc ánh sáng được tính bởi công thức \(I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }}\), trong đó Im là cường độ ánh sáng đã chiếu lên màn lọc ánh sáng và là góc \(\alpha \) như trong Hình 1.21 (nguồn: http://www.vedantu.com/iit-jee/malus-law). Chứng minh rằng: \(I = {I_m}{\cos ^2}\alpha \).

Phương pháp giải:
Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
\(\begin{array}{l}I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }} = {I_m}\left( {1 - \frac{1}{{1 + {{\cot }^2}\alpha }}} \right) = {I_m}.\left( {1 - \frac{1}{{\frac{1}{{{{\sin }^2}\alpha }}}}} \right)\\ = {I_m}.\left( {1 - {{\sin }^2}\alpha } \right) = {I_m}.{\cos ^2}\alpha \end{array}\)
Hoạt động 4
a) Dựa vào Hình 1.22, hãy so sánh \(\cos \left( { - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \(\sin \left( { - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( { - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( { - \alpha } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.22, ta thấy:
\(\cos \left( { - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\(\sin \left( { - \alpha } \right) = - \sin \left( \alpha \right)\)
b)
\(\begin{array}{l}\tan \left( { - \alpha } \right) = \frac{{\sin \left( { - \alpha } \right)}}{{\cos \left( { - \alpha } \right)}} = \frac{{ - \sin \alpha }}{{\cos \alpha }} = - \tan \alpha \\\cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} = - \cot \alpha \end{array}\)
Hoạt động 5
a) Dựa vào Hình 1.23, hãy so sánh \(\sin \left( {\pi - \alpha } \right)\) và \(\sin \left( \alpha \right)\); \(\cos \left( {\pi - \alpha } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\pi - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\pi - \alpha } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.23, ta thấy:
\(\sin \left( {\pi - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
\(\cos \left( {\pi - \alpha } \right) = - \cos \left( \alpha \right)\)
b) \(\tan \left( {\pi - \alpha } \right) = \frac{{\sin \left( {\pi - \alpha } \right)}}{{\cos \left( {\pi - \alpha } \right)}} = \frac{{\sin \alpha }}{{ - \cos \alpha }} = - \tan \alpha \)
\(\cot \left( {\pi - \alpha } \right) = \frac{1}{{\tan \left( {\pi - \alpha } \right)}} = \frac{1}{{ - \tan \alpha }} = - \cot \alpha \)
Hoạt động 6
a) Dựa vào Hình 1.24, hãy so sánh \(\sin \left( {\alpha + \pi } \right)\) và \(\sin \left( \alpha \right)\); \({\rm{cos}}\left( {\alpha + \pi } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\alpha + \pi } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\alpha + \pi } \right)\) và \(\cot \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.24, ta thấy:
\(\sin \left( {\alpha + \pi } \right) = - \sin \alpha \)
\({\rm{cos}}\left( {\alpha + \pi } \right) = - \cos \alpha \)
b) \(\tan \left( {\alpha + \pi } \right) = \frac{{\sin \left( {\alpha + \pi } \right)}}{{\cos \left( {\alpha + \pi } \right)}} = \frac{{ - \sin \alpha }}{{ - \cos \alpha }} = \tan \alpha \)
\(\cot \left( {\alpha + \pi } \right) = \frac{{\cos \left( {\alpha + \pi } \right)}}{{\sin \left( {\alpha + \pi } \right)}} = \frac{{ - \cos \alpha }}{{ - \sin \alpha }} = \cot \alpha \)
Hoạt động 7
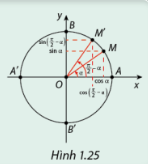
a) Dựa vào Hình 1.25, hãy so sánh \(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cot \left( \alpha \right)\); \(\cot \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\tan \left( \alpha \right)\).

Phương pháp giải:
a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.
Lời giải chi tiết:
a) Dựa vào Hình 1.25, ta thấy:
\(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
b) \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \)
\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}}{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha \)
Luyện tập 5
Chứng minh giá trị của biểu thức sau không phụ thuộc \(\alpha \):
\(B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\)
Phương pháp giải:
Áp dụng các hệ thức giữa giá trị lượng giác của các góc lượng giác có liên quan đặc biệt.
Lời giải chi tiết:
\(\begin{array}{l}B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\\ \Leftrightarrow B = {\left( { - \sin \alpha } \right)^2} + {\cos ^2}\alpha + \cos \alpha - \cos \alpha \\ \Leftrightarrow B = {\sin ^2}\alpha + {\cos ^2}\alpha \\ \Leftrightarrow B = 1\end{array}\)
Vậy B không phụ thuộc \(\alpha \).
Giải mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Hướng dẫn chi tiết
Mục 2 trong SGK Toán 11 tập 1 thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2, trang 11, 12, 13, 14, 15, giúp các em học sinh hiểu rõ hơn về các khái niệm và kỹ năng cần thiết.
Nội dung chính của Mục 2 SGK Toán 11 tập 1
- Định nghĩa hàm số bậc hai: Hàm số có dạng y = ax2 + bx + c, với a ≠ 0.
- Tính chất của hàm số bậc hai: Tập xác định, tập giá trị, tính đơn điệu, cực trị.
- Đồ thị hàm số bậc hai (Parabol): Đỉnh, trục đối xứng, điểm cắt trục hoành, điểm cắt trục tung.
- Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế liên quan đến quỹ đạo, diện tích, tối ưu hóa.
Giải chi tiết các bài tập trang 11, 12, 13, 14, 15
Bài 1 (Trang 11): Xác định hệ số a, b, c của hàm số
Bài tập này yêu cầu các em xác định các hệ số a, b, c trong hàm số bậc hai đã cho. Ví dụ, nếu hàm số là y = 2x2 - 3x + 1, thì a = 2, b = -3, c = 1.
Bài 2 (Trang 12): Tìm tập xác định của hàm số
Tập xác định của hàm số bậc hai là tập hợp tất cả các số thực, trừ các giá trị làm mẫu số bằng 0 (nếu có). Trong hầu hết các trường hợp, tập xác định là R.
Bài 3 (Trang 13): Vẽ đồ thị hàm số
Để vẽ đồ thị hàm số bậc hai, các em cần xác định:
- Đỉnh của parabol: I(x0, y0) với x0 = -b/2a, y0 = f(x0).
- Trục đối xứng: x = x0.
- Điểm cắt trục tung: A(0, c).
- Điểm cắt trục hoành (nếu có): Giải phương trình ax2 + bx + c = 0.
Sau khi xác định các điểm này, các em có thể vẽ đồ thị parabol.
Bài 4 (Trang 14): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Nếu a > 0, hàm số có giá trị nhỏ nhất tại đỉnh parabol. Nếu a < 0, hàm số có giá trị lớn nhất tại đỉnh parabol.
Bài 5 (Trang 15): Giải phương trình bậc hai
Sử dụng công thức nghiệm của phương trình bậc hai: x = (-b ± √(b2 - 4ac)) / 2a.
Lời khuyên khi học tập
Để học tốt môn Toán 11, các em cần:
- Nắm vững kiến thức cơ bản về hàm số, phương trình, bất phương trình.
- Luyện tập thường xuyên các bài tập để rèn luyện kỹ năng giải toán.
- Tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.
- Sử dụng các tài liệu tham khảo, sách bài tập để mở rộng kiến thức.
Tusach.vn hy vọng rằng bài viết này sẽ giúp các em học sinh giải quyết các bài tập trong mục 2 trang 11, 12, 13, 14, 15 SGK Toán 11 tập 1 một cách hiệu quả. Chúc các em học tập tốt!