Giải mục 3 trang 26, 27, 28, 29, 30 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 26, 27, 28, 29, 30 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 26, 27, 28, 29, 30 SGK Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của từng bài toán, từ đó nâng cao khả năng tự học và giải quyết vấn đề.
a) Xét các số thực x1, x2, sao cho \(0 < {x_1} < {x_2} < \frac{\pi }{2}\). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x1 rad và x2 rad. Hãy so sánh tung độ của M và N, từ đó so sánh \(\sin {x_1}\) và \(\sin {x_2}\).
Hoạt động 7
a) Xét các số thực x1, x2, sao cho \(0 < {x_1} < {x_2} < \frac{\pi }{2}\). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x1 rad và x2 rad. Hãy so sánh tung độ của M và N, từ đó so sánh \(\sin {x_1}\) và \(\sin {x_2}\).
b) Xét các số thực x3, x4, sao cho \(\frac{\pi }{2} < {x_1} < {x_2} < \pi \). Gọi P và Q lần lượt là điểm biểu diễn của góc lượng giác có số đo x3 rad và x4 rad. Hãy so sánh tung độ của P và Q, từ đó so sánh \(\sin {x_3}\) và \(\sin {x_4}\).
Phương pháp giải:
Lấy x1, x2 và x3, x4 bất kì thỏa mãn yêu cầu của đề bài. Tung độ của các điểm M, N, P, Q chính là \(\sin {x_1}\), \(\sin {x_2}\), \(\sin {x_3}\), \(\sin {x_4}\). Tính \(\sin {x_1}\), \(\sin {x_2}\), \(\sin {x_3}\), \(\sin {x_4}\). Từ đó so sánh các giá trị này.
Lời giải chi tiết:
a)
\(\begin{array}{l}{x_1} = \frac{\pi }{6} \Rightarrow \sin \frac{\pi }{6} = \frac{1}{2}\\{x_2} = \frac{\pi }{3} \Rightarrow \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\ \Rightarrow \sin {x_1} < \sin {x_2}\end{array}\)
b)
\(\begin{array}{l}{x_3} = \frac{{2\pi }}{3} \Rightarrow \sin \frac{{2\pi }}{3} = \frac{{\sqrt 3 }}{2}\\{x_4} = \frac{{5\pi }}{6} \Rightarrow \sin \frac{{5\pi }}{6} = \frac{1}{2}\\ \Rightarrow \sin {x_3} > \sin {x_4}\end{array}\)
Luyện tập 7
a) Dựa vào đồ thị hàm số \(y = \sin x\), xác định tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\sin x = 0\).
b) Xác định các khoảng nghịch biến của hàm số \(y = \sin x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \sin x\).
Lời giải chi tiết:
a) Dựa vào đồ thị hàm số \(y = \sin x\) trên đoạn \(x \in \left[ { - 3\pi ;3\pi } \right]\), ta có \(\sin x = 0\) khi \(x \in \left\{ { - 3\pi ; - 2\pi ; - \pi ;0;\pi ;2\pi ;3\pi } \right\}\).
b) Các khoảng nghịch biến của hàm số \(y = \sin x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\) là \(\left( { - 3\pi ; - \frac{{5\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
Hoạt động 8
Xét các số thực x1, x2 sao cho \(0 < {x_1} < {x_2} < \pi \). Gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo x1 rad và x2 rad. Hãy so sánh hoành độ của M và N, từ đó so sánh \(\cos {x_1}\) và \(\cos {x_2}\).
Phương pháp giải:
Lấy x1, x2 bất kì thỏa mãn yêu cầu của đề bài. Hoành độ của các điểm M, N chính là \(\cos {x_1},\cos {x_2}\). Tính \(\cos {x_1},\cos {x_2}\). Từ đó so sánh các giá trị này.
Lấy x1, x2 bất kì thỏa mãn yêu cầu của đề bài. Hoành độ của các điểm M, N chính là \(\cos {x_1},\cos {x_2}\). Tính \(\cos {x_1},\cos {x_2}\). Từ đó so sánh các giá trị này.
Lời giải chi tiết:
\(\begin{array}{l}{x_1} = \frac{\pi }{6} \Rightarrow \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\\{x_2} = \frac{\pi }{4} \Rightarrow \cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \cos {x_1} > \cos {x_2}\end{array}\)
Luyện tập 8
a) Dựa vào đồ thị hàm số \(y = \cos x\), xác định tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\cos x = - 1\).
b) Xác định các khoảng nghịch biến của hàm số \(y = \cos x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \cos x\).
Lời giải chi tiết:

a) Dựa vào đồ thị hàm số \(y = \cos x\), tất cả các giá trị của \(x \in \left[ { - 3\pi ;3\pi } \right]\) sao cho \(\cos x = - 1\) là \( - 3\pi , - \pi ,\pi ,3\pi \).
b) Các khoảng nghịch biến của hàm số \(y = \cos x\) trên đoạn \(\left[ { - 3\pi ;3\pi } \right]\) là \(\left( { - 2\pi ; - \pi } \right),\left( {0;\pi } \right),\left( {2\pi ;3\pi } \right)\).
Vận dụng 2
Giả sử nhiệt độ bên trong một ngôi nhà sau t giờ kể từ 12 giờ trưa, gọi là \(T\left( t \right)\), được tính bởi công thức: \(T\left( t \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi t}}{6}} \right) + 25\left( {^0C} \right)\), \(0 \le t \le 24\).
a) Tìm nhiệt độ bên trong ngôi nhà lúc 12 giờ trưa, 6 giờ tối, 12 giờ đêm theo công thức trên.
b) Theo công thức trên, nhiệt độ cao nhất bên trong ngôi nhà là bao nhiêu?
Phương pháp giải:
a) t giờ được tính kể từ 12 giờ trưa nên t lúc 12 giờ trưa bằng 0, lúc 6 giờ tối bằng 6, lúc 12 giờ đêm bằng 12. Thay t = 0, 6, 12 lần lượt vào công thức.
b) Dựa vào \(\cos a \le 1\forall a\) để lập luận.
Lời giải chi tiết:
a) \(T\left( 0 \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .0}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
\(T\left( 6 \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .6}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
\(T\left( {12} \right) = 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) + 25 = 25\left( {^0C} \right)\)
Vậy nhiệt độ bên trong ngôi nhà lúc 12 giờ trưa, 6 giờ tối, 12 giờ đêm đều là \({25^0}C\).
b)
\(\begin{array}{l}\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) \le 1\forall t\\ \Leftrightarrow 5\cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) \le 5\forall t\\ \Leftrightarrow \cos \left( {\frac{\pi }{2} - \frac{{\pi .12}}{6}} \right) + 25 \le 30\forall t\end{array}\)
Vậy nhiệt độ cao nhất trong nhà là \({30^0}C\).
Hoạt động 9
a) Chép lại và hoàn thành bảng sau:
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | ? | ? | ? |
b) So sánh \(\tan \frac{\pi }{6},\tan \frac{\pi }{4}\) và \(\tan \frac{\pi }{3}\).
Phương pháp giải:
Thay \(x = \frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3}\) vào \(\tan x\) để tính rồi so sánh.
Lời giải chi tiết:
a)
x | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | \(\frac{{\sqrt 3 }}{3}\) | 1 | \(\sqrt 3 \) |
b) \(\tan \frac{\pi }{6} < \tan \frac{\pi }{4} < \tan \frac{\pi }{3}\).
Luyện tập 9
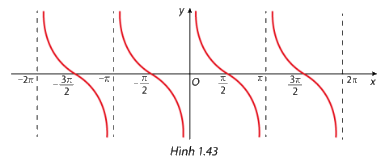
Xác định các khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \tan x\).
Lời giải chi tiết:

Khoảng đồng biến của hàm số \(y = \tan x\) trên \(\left( { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right)\backslash \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\) là \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right),\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right),\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Hoạt động 10
a) Chép lại và hoàn thành bảng sau:

b) So sánh các giá trị của trong bảng trên.
Phương pháp giải:
Thay \(x = \frac{\pi }{6},\frac{\pi }{4},\frac{\pi }{3},\frac{\pi }{2},\frac{{2\pi }}{3},\frac{{3\pi }}{4},\frac{{5\pi }}{6}\) vào \(\cot x\) để tính rồi so sánh.
Lời giải chi tiết:
a)

b) \(\cot \frac{\pi }{6} > \cot \frac{\pi }{4} > \cot \frac{\pi }{3} > \cot \frac{{2\pi }}{3} > \cot \frac{{3\pi }}{4} > \cot \frac{{5\pi }}{6}\)
Luyện tập 10
Xác định các khoảng nghịch biến của hàm số \(y = \cot x\) trên \(\left( { - 2\pi ;2\pi } \right)\backslash \left\{ { - \pi ;0;\pi } \right\}\).
Phương pháp giải:
Quan sát đồ thị hàm số \(y = \cot x\).
Lời giải chi tiết:

Các khoảng nghịch biến của hàm số \(y = \cot x\) trên \(\left( { - 2\pi ;2\pi } \right)\backslash \left\{ { - \pi ;0;\pi } \right\}\) là \(\left( { - 2\pi ; - \pi } \right),\left( { - \pi ,0} \right),\left( {0;\pi } \right),\left( {\pi ;2\pi } \right)\).
Giải mục 3 trang 26, 27, 28, 29, 30 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Phương pháp giải
Mục 3 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Nội dung chính của Mục 3
- Phép tịnh tiến: Định nghĩa, tính chất, và ứng dụng trong việc giải các bài toán hình học.
- Phép quay: Định nghĩa, tính chất, và cách xác định tâm quay, góc quay.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định trục đối xứng.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định tâm đối xứng.
- Kết hợp các phép biến hình: Cách thực hiện và ứng dụng của việc kết hợp các phép biến hình.
Phương pháp giải bài tập hiệu quả
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các kết quả cần tìm.
- Vẽ hình: Vẽ hình minh họa giúp hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Áp dụng định nghĩa và tính chất: Sử dụng các định nghĩa, tính chất của các phép biến hình để giải bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Giải chi tiết các bài tập trang 26, 27, 28, 29, 30
Bài 1 (Trang 26):
(Giả sử đây là một bài tập về phép tịnh tiến)
Lời giải: Để tịnh tiến điểm M theo vectơ v, ta thực hiện phép cộng vectơ: M' = M + v. Thay tọa độ của M và v vào, ta tính được tọa độ của M'.
Bài 2 (Trang 27):
(Giả sử đây là một bài tập về phép quay)
Lời giải: Xác định tâm quay O và góc quay α. Sử dụng công thức quay điểm quanh tâm O để tìm tọa độ của điểm M' sau khi quay.
Bài 3 (Trang 28):
(Giả sử đây là một bài tập về phép đối xứng trục)
Lời giải: Tìm ảnh của điểm M qua phép đối xứng trục d. Sử dụng tính chất đối xứng để xác định tọa độ của M'.
Bài 4 (Trang 29):
(Giả sử đây là một bài tập về phép đối xứng tâm)
Lời giải: Tìm ảnh của điểm M qua phép đối xứng tâm I. Sử dụng tính chất đối xứng để xác định tọa độ của M'.
Bài 5 (Trang 30):
(Giả sử đây là một bài tập kết hợp các phép biến hình)
Lời giải: Thực hiện các phép biến hình theo thứ tự được yêu cầu trong đề bài. Sử dụng công thức biến hình tương ứng để tìm tọa độ của điểm cuối cùng.
Lưu ý quan trọng
Trong quá trình giải bài tập, hãy chú ý đến việc sử dụng đúng công thức và tính chất của các phép biến hình. Đừng quên kiểm tra lại kết quả để đảm bảo tính chính xác. Nếu gặp khó khăn, hãy tham khảo các tài liệu tham khảo hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ học tốt môn Toán 11 và đạt được kết quả cao trong các kỳ thi.