Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám phá
SGK Toán 11 - Cùng khám phá
Toán 11 tập 1 - Cùng khám phá
Chương 2 Dãy số. Cấp số cộng. Cấp số nhân
Bài 3. Cấp số nhân

Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám phá

Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám phá

Chào mừng bạn đến với lời giải chi tiết bài tập mục 2 trang 54 SGK Toán 11 tập 1 trên tusach.vn. Bài viết này sẽ cung cấp cho bạn đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn hiểu sâu hơn về kiến thức Toán học.

Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp bạn học Toán 11 một cách hiệu quả nhất.

Một quả bóng được ném xuống từ độ cao 3 m. Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó (Hình 2.8).

Hoạt động 2Luyện tập 2

Hoạt động 2

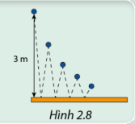
    Một quả bóng được ném xuống từ độ cao 3 m. Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó (Hình 2.8). Tính độ cao của lần nảy lên thứ nhất, thứ hai, thứ ba, thứ năm.

    Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám phá 1

    Phương pháp giải:

    - Dựa vào đầu bài, xác định \({u_1},q\).

    - Áp dụng công thức \({u_{n + 1}} = {u_n}.q\).

    Lời giải chi tiết:

    Độ cao mà quả bóng nảy lên bằng \(\frac{3}{5}\) độ cao trước đó nên ta lập được cấp số nhân với \(q = \frac{3}{5}\). Độ cao lần nảy thứ nhất là \(3.\frac{3}{5} = \frac{9}{5}\)\({u_1} = 3\) nên \({u_1} = \frac{9}{5}\).

    \( \Rightarrow {u_2} = \frac{9}{5}.\frac{3}{5} = \frac{{27}}{{25}};{u_3} = \frac{{27}}{{25}}.\frac{3}{5} = \frac{{81}}{{125}};{u_4} = \frac{{81}}{{125}}.\frac{3}{5} = \frac{{243}}{{625}};{u_5} = \frac{{243}}{{625}}.\frac{3}{5} = \frac{{729}}{{3125}}\)

    Vậy độ cao của lần thứ nhất là \(\frac{9}{5}\) m, lần thứ hai là \(\frac{{27}}{{25}}\) m, lần thứ ba là \(\frac{{81}}{{125}}\) m, lần thứ năm là \(\frac{{729}}{{3125}}\) m.

    Luyện tập 2

      Một nước có dân số 25 triệu người vào đầu năm 2001. Nếu tỉ lệ tăng dân số hàng năm ổn định là 0,5%, tính dân số của nước đó vào đầu năm 2040.

      Phương pháp giải:

      Dựa vào đầu bài, xác định \({u_1},q,n\).

      Áp dụng công thức: \({u_n} = {u_1}.{q^{n - 1}}\left( {n \ge 2} \right)\).

      Lời giải chi tiết:

      Gọi \({u_1}\) là dân số năm 2001, \({u_2}\) là dân số năm 2002.

      \( \Rightarrow {u_1} = 25;{u_2} = 25 + 0,5\% .25 = 25,125\)

      \( \Rightarrow q = \frac{{{u_2}}}{{{u_1}}} = \frac{{25,125}}{{25}} = 1,005\)

      Tương tự như vậy với \({u_3},{u_4},...\) Ta sẽ lập được cấp số nhân với \({u_1} = 25,q = 1,005\).

      Vậy dân số của nước đó vào năm 2040 là: \({u_{39}} = {u_1}.{q^{38}} = 25.1,{005^{38}} \approx 30\) (triệu người).

      Giải mục 2 trang 54 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Phương pháp

      Mục 2 trang 54 SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, đặc biệt là phép tịnh tiến và phép đối xứng. Việc nắm vững lý thuyết và phương pháp giải các bài tập liên quan là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các kiến thức Toán học nâng cao hơn.

      1. Lý thuyết cần nắm vững

      • Phép tịnh tiến: Định nghĩa, tính chất, biểu thức tọa độ của phép tịnh tiến.
      • Phép đối xứng trục: Định nghĩa, tính chất, biểu thức tọa độ của phép đối xứng trục.
      • Phép đối xứng tâm: Định nghĩa, tính chất, biểu thức tọa độ của phép đối xứng tâm.
      • Mối quan hệ giữa các phép biến hình: Cách kết hợp các phép biến hình để tạo ra một phép biến hình mới.

      2. Các dạng bài tập thường gặp

      1. Xác định ảnh của một điểm hoặc một hình qua phép biến hình: Đây là dạng bài tập cơ bản, yêu cầu học sinh vận dụng công thức tọa độ để tìm ra ảnh của điểm hoặc hình sau khi thực hiện phép biến hình.
      2. Tìm phép biến hình thỏa mãn điều kiện cho trước: Dạng bài tập này đòi hỏi học sinh phải suy luận và kết hợp các tính chất của phép biến hình để tìm ra phép biến hình phù hợp.
      3. Chứng minh một đẳng thức liên quan đến phép biến hình: Học sinh cần sử dụng các tính chất của phép biến hình và các công thức tọa độ để chứng minh đẳng thức.
      4. Ứng dụng phép biến hình vào giải quyết các bài toán hình học: Đây là dạng bài tập nâng cao, yêu cầu học sinh phải vận dụng kiến thức về phép biến hình để giải quyết các bài toán hình học phức tạp.

      3. Giải chi tiết bài tập mục 2 trang 54 SGK Toán 11 tập 1

      Để giúp bạn hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 54 SGK Toán 11 tập 1, chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập:

      Bài 1: (Giả sử đây là nội dung bài tập)...

      Lời giải:...

      Bài 2: (Giả sử đây là nội dung bài tập)...

      Lời giải:...

      4. Mẹo giải nhanh và hiệu quả

      • Nắm vững các công thức tọa độ của các phép biến hình.
      • Vẽ hình minh họa để dễ dàng hình dung bài toán.
      • Sử dụng các tính chất của phép biến hình để đơn giản hóa bài toán.
      • Kiểm tra lại kết quả sau khi giải xong.

      5. Luyện tập thêm

      Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 tập 1 hoặc trên các trang web học Toán trực tuyến.

      Bảng tổng hợp các công thức quan trọng:

      Phép biến hìnhCông thức tọa độ
      Tịnh tiếnx' = x + a, y' = y + b
      Đối xứng trục Oyx' = -x, y' = y
      Đối xứng tâm Ox' = -x, y' = -y

      Hy vọng với những kiến thức và lời giải chi tiết trên, bạn sẽ tự tin hơn khi giải các bài tập mục 2 trang 54 SGK Toán 11 tập 1. Chúc bạn học tập tốt!

      Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

      CHỦ ĐỀ SÁCH XEM NHIỀU

      Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

      VỀ TUSACH.VN