A. Lý thuyết
1. Biến cố độc lập
| Hai biến cố được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia. |
Nhận xét: Nếu A và B là hai biến cố độc lập thì:
- A và \(\overline B \) là hai biến cố độc lập.
- \(\overline A \) và B là hai biến cố độc lập.
- \(\overline A \) và \(\overline B \) là hai biến cố độc lập.
2. Công thức nhân xác suất của hai biến cố độc lập
Nếu A và B là hai biến cố độc lập thì P(AB) = P(A).P(B). |
Lưu ý: Nếu \(P(AB) \ne P(A).P(B)\) thì A và B không độc lập.
3. Sử dụng công thức tổ hợp và sơ đồ hình cây tính xác suất
B. Bài tập
Bài 1: Gieo đồng thời hai con xúc xắc cần đối đồng chất, một màu đỏ một màu xanh và quan sát số chấm xuất hiện trên hai con xúc xắc. Gọi A là biến cố "Số chấm trên mặt xuất hiện của xúc xắc màu đỏ là chẵn" và B là biến cố "Số chấm trên mặt xuất hiện của xúc xắc màu xanh là lẻ". Chỉ ra một cặp biến cố độc lập của phép thử trong và tính xác suất của các biến cố đó.
Giải:
Xét cặp biến cố sau:
A: "Xúc xác màu đỏ xuất hiện mặt 6 chấm".
B: "Xúc xác màu xanh xuất hiện mặt một chấm".
Số phần tử của không gian mẫu, biến cố A và biến cố B lần lượt là:
n(Ω) = 6.6 = 36; n(A) = 6; n(B) = 6.
Do số chấm xuất hiện trên con xúc xác màu đỏ không phụ thuộc vào số chấm xuất hiện trên con xúc xác màu xanh và ngược lại nên việc xảy ra hay không xảy ra biến cố A không làm ảnh hưởng đến xác suất của biến cố B và ngược lại. Do đó biến cố A và B là độc lập. Xác suất của biến cố A và B lần lượt là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\); \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}\).
Bài 2: Có hai giỏ trái cây chứa hai loại táo xanh và táo đỏ. Giỏ thứ nhất chứa 5 quả táo xanh và 5 quả táo đỏ. Giỏ thứ hai chứa 4 quả táo xanh và 6 quả táo đỏ. Từ mỗi giỏ lấy ngẫu nhiên một quả táo.
Xét các biến cố:
A: "Quả táo lấy ra từ giỏ thứ nhất màu đỏ".
B: "Quả táo lấy ra từ giỏ thứ hai màu đỏ".
a) Tính P(A), P(B) và P(AB).
b) Tính xác suất để trong hai quả táo lấy ra có ít nhất một quả màu xanh.
Giải:
a) Số phần tử không gian mẫu là n(Ω) = 10.10 = 100.
Số phần tử của biến cố A và B lần lượt là n(A) = 5.10 = 50; n(B) = 6.10 = 60.
Xác suất của các biến cố A và B lần lượt là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{50}}{{100}} = 0,5\); \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{60}}{{100}} = 0,6\).
Do A và B là hai biến cố độc lập nên P(AB) = P(A).P(B) = 0,5.0,6 = 0,3.
b) Gọi C là biến cố "Hai quả táo lấy ra có ít nhất một quả màu xanh". Khi đó, C là biến cố đối của biến cố AB. Xác suất trong hai quả táo lấy ra có ít nhất một quả màu xanh là:
\(P(C) = P(\overline {AB} ) = 1 - P(AB) = 1 - 0,3 = 0,7\).
Bài 3: Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa 4 quả cầu xanh, 4 quả cầu đỏ và 4 quả cầu vàng. Hộp thứ hai chứa 5 quả cầu xanh, 5 quả cầu đỏ và 5 quả cầu vàng. Lấy ngẫu nhiên từ mỗi hộp 3 quả cầu. Tính xác suất để lấy được 6 quả cầu đỏ.
Giải:
Xét các biến cố:
A: "Ba quả cầu trong hộp thứ nhất là màu đỏ";
B: "Ba quả cầu trong hộp thứ hai là màu đỏ".
Số phần tử của không gian mẫu Ω và các biến cố A, B lần lượt là:
\(n(\Omega ) = C_{12}^3.C_{15}^3\); \(n(A) = C_4^3.C_{15}^3\); \(n(B) = C_5^3.C_{12}^3\).
Xác suất của các biến cố A, B lần lượt là P(A) và P(B):
\(P(A) = \frac{{C_4^3.C_{15}^3}}{{C_{12}^3.C_{15}^3}} = \frac{4}{{220}} = \frac{1}{{55}}\); \(P(A) = \frac{{C_5^3.C_{12}^3}}{{C_{12}^3.C_{15}^3}} = \frac{{10}}{{445}} = \frac{2}{{91}}\).
Do A và B là hai biến cố độc lập nên xác suất để lấy được 6 quả cầu đỏ là:
\(P(AB) = P(A).P(B) = \frac{1}{{55}}.\frac{2}{{91}} = \frac{2}{{5005}}\).
Bài 4: Minh và Nam lần lượt thực hiện một cú sút vào khung thành. Xác suất để Minh sút thành công vào khung thành là 0,6 và Nam sút thành công vào khung thành là 0,7. Sơ đồ cây chưa hoàn thiện bên dưới mô tả các khả năng xảy ra và xác suất tương ứng khi hai bạn lần lượt thực hiện cú sút.
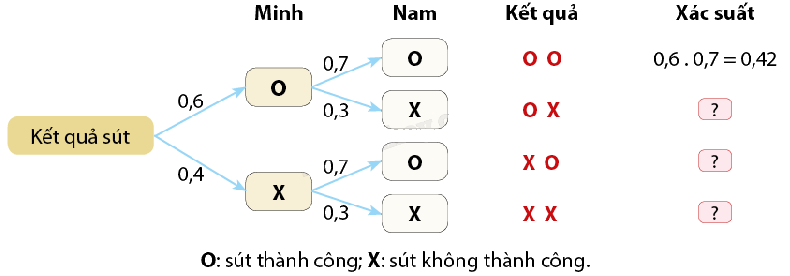
a) Hoàn thiện ba dòng trong cột cuối cùng của sơ đồ hình cây.
b) Tính xác suất để cả hai bạn không sút thành công.
c) Tính xác suất để ít nhất một bạn sút thành công.
Giải:
a) Các phép tính trên ba dòng trong cột cuối cùng của sơ đồ hình cây theo thứ tự là:
0,6.0,3 = 0,18;
0,4.0,7 = 0,28;
0,4.0,3 = 0,12.
b) Xác suất để cả hai bạn không sút thành công là 0,12.
c) Xác suất để có ít nhất một bạn sút thành công là:
0,42 + 0,18 + 0,28 = 0,88.