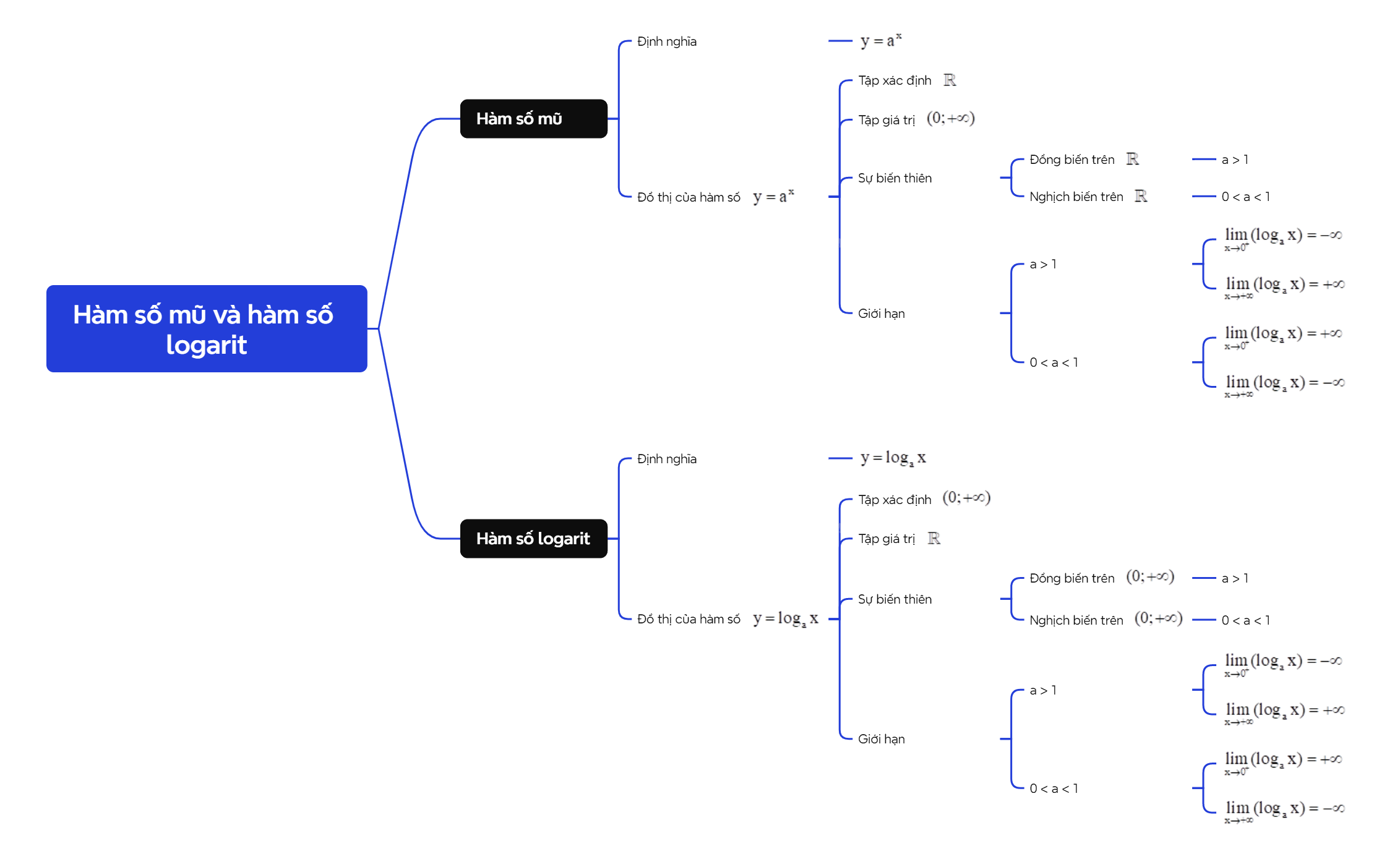
A. Lý thuyết
1. Hàm số mũ
a) Định nghĩa
| Cho a là một số thực dương và khác 1. Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a. |
Lưu ý:
- Hàm số \(y = {a^x}\) \((a > 0,a \ne 1)\) có tập xác định là \(\mathbb{R}\) và tập giá trị là \((0; + \infty )\).
- Hàm số \(y = {a^x}\) liên tục trên \(\mathbb{R}\).
- Với a = 1 thì \({1^x} = 1\) với mọi \(x \in \mathbb{R}\).
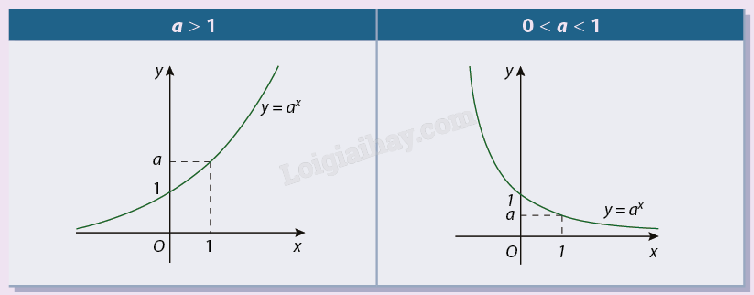
b) Đồ thị của hàm số \(y = {a^x}\) \((a > 0,a \ne 1)\)
Hàm số mũ \(y = {a^x}\) \((a > 0,a \ne 1)\) có tập xác định là \(\mathbb{R}\) và tập giá trị là \((0; + \infty )\). Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1. Với a > 1 thì \(\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } {a^x} = + \infty \). Với 0 < a < 1 thì \(\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty \); \(\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0\). Đồ thị (C) của hàm số \(y = {a^x}\) luôn nằm phía trên trục hoành, luôn đi qua các điểm (0;1) và (1;a). |
2. Hàm số logarit
a) Định nghĩa
| Cho số thực dương a khác 1. Hàm số \(y = {\log _a}x\) được gọi là hàm số logarit cơ số a. |
Lưu ý:
- Hàm số \(y = {\log _a}x\) có tập xác định là \(D = (0; + \infty )\) và tập giá trị là \(\mathbb{R}\).
- Hàm số \(y = {\log _a}x\) liên tục trên khoảng \(D = (0; + \infty )\).
- Hàm số \(y = {\log _a}(u(x))\) \((a > 0,a \ne 1)\) xác định khi và chỉ khi u(x) xác định và u(x) > 0.
b) Đồ thị của hàm số logarit \(y = {\log _a}(u(x))\) \((a > 0,a \ne 1)\)
Hàm số logarit \(y = {\log _a}x\) \((a > 0,a \ne 1)\) có tập xác định là \((0; + \infty )\) và tập giá trị là \(\mathbb{R}\). Hàm số \(y = {\log _a}x\) đồng biến trên \((0; + \infty )\) khi a > 1 và nghịch biến trên \((0; + \infty )\) khi 0 < a < 1. Với a > 1 thì \(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _a}x) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } ({\log _a}x) = + \infty \). Với 0 < a < 1 thì \(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _a}x) = + \infty \); \(\mathop {\lim }\limits_{x \to + \infty } ({\log _a}x) = - \infty \). Đồ thị (C) của hàm số \(y = {\log _a}x\) luôn nằm phía bên phải trục tung, luôn đi qua các điểm (1;0) và (a;1). |

B. Bài tập
Bài 1: Hàm số nào sau đây là hàm số mũ? Tìm cơ số của hàm số mũ đó.
a) \(y = {2^x}\).
b) \(y = {(\sqrt 2 - 1)^x}\).
c) \(y = {e^x}\).
d) \(y = {x^e}\).
Giải:
a) Hàm số \(y = {2^x}\) là hàm số mũ với cơ số bằng 2.
b) Hàm số \(y = {(\sqrt 2 - 1)^x}\) là hàm số mũ với cơ số bằng \(\sqrt 2 - 1\).
c) Hàm số \(y = {e^x}\) là hàm số mũ với cơ số bằng e.
d) Hàm số \(y = {x^e}\) không phải là hàm số mũ vì cơ số không phải hằng số.
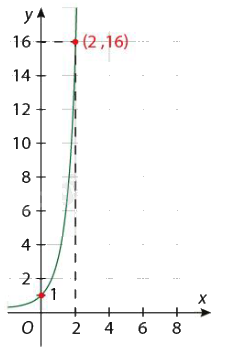
Bài 2: Tìm hàm số mũ \(f(x) = {a^x}\) mà dồ thị của nó được cho bên dưới:
a)
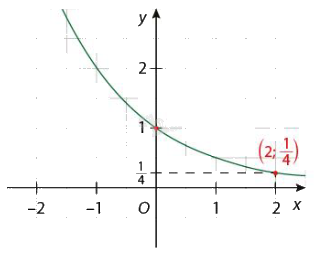
b)
Giải:
a) Vì \(f(x) = {a^2} = 16\) nên a = 4. Do đó \(f(x) = {4^x}\).
b) Vì \(f(x) = {a^2} = \frac{1}{4}\) nên \(a = \frac{1}{2}\). Do đó \(f(x) = {\left( {\frac{1}{2}} \right)^x}\).
Bài 3: Xác định cơ số của các hàm số logarit sau:
a) \(y = {\log _3}x\).
b) \(y = \ln x\).
c) \(y = \log x\).
Giải:
a) Hàm số \(y = {\log _3}x\) có cơ số bằng 3.
b) Hàm số \(y = \ln x\) có cơ số bằng e.
c) Hàm số \(y = \log x\) có cơ số bằng 10.
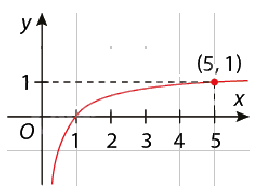
Bài 4: Tìm hàm số logarit \(f(x) = {\log _a}x\) mà đồ thị của nó được cho bên dưới:
a)
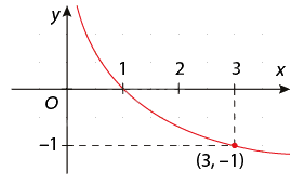
b)
Giải:
a) Vì f(5) = 1 nên \({\log _a}5 = 1 \Leftrightarrow a = 5\). Do đó \(f(x) = {\log _5}x\).
b) Vì f(3) = -1 nên \({\log _a}3 = - 1 \Leftrightarrow a = \frac{1}{3}\). Do đó \(f(x) = {\log _{\frac{1}{3}}}x\).