Lý thuyết Hai đường thẳng vuông góc - SGK Toán 11 Cùng khám phá

Tổng quan nội dung

Lý thuyết Hai Đường Thẳng Vuông Góc - SGK Toán 11

Bài học về hai đường thẳng vuông góc là một phần quan trọng trong chương trình Toán 11, giúp học sinh nắm vững kiến thức về vectơ, phương trình đường thẳng và mối quan hệ giữa chúng.

Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu, giúp bạn tự tin chinh phục kiến thức này.

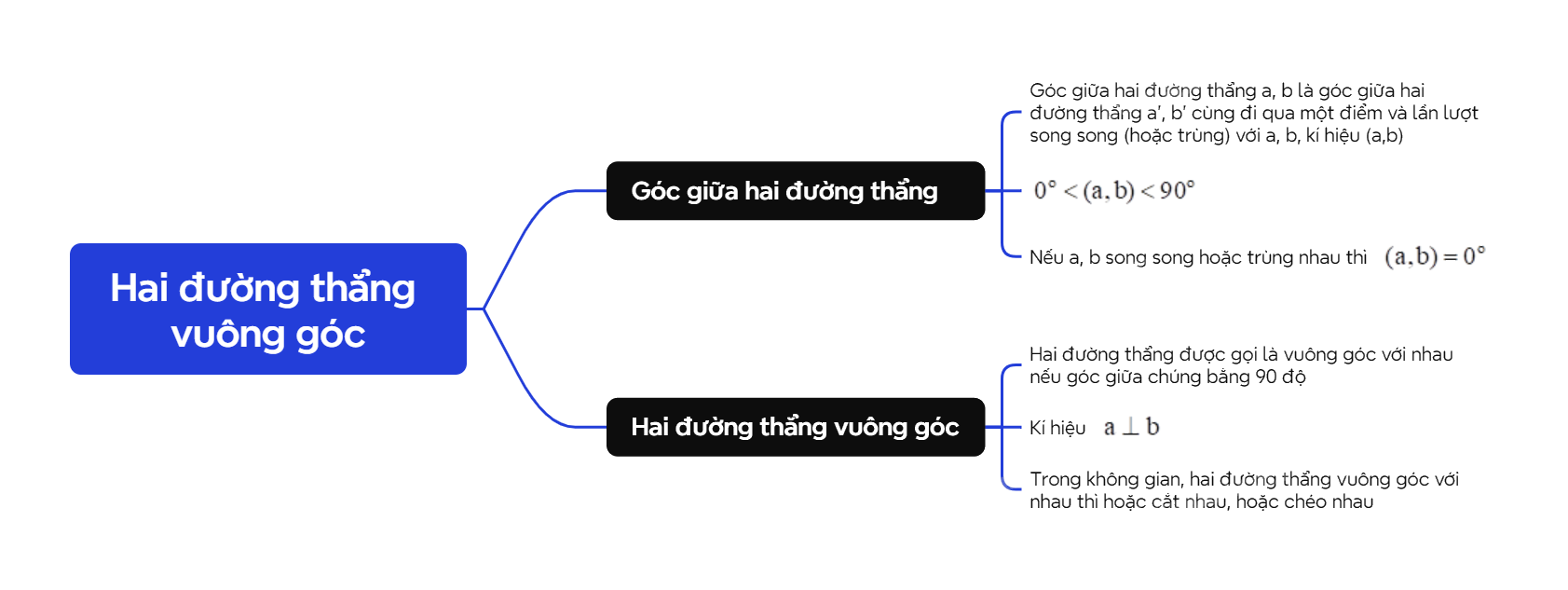
A. Lý thuyết 1. Góc giữa hai đường thẳng

A. Lý thuyết

1. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng a, b là góc giữa hai đường thẳng a’, b’ cùng đi qua một điểm và lần lượt song song (hoặc trùng) với a, b, kí hiệu (a,b).

Nhận xét:

+ \({0^o} < (a,b) < {90^o}\).

+ Nếu a, b song song hoặc trùng nhau thì \((a,b) = {0^o}\).

2. Hai đường thẳng vuông góc

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^o}\).

Lưu ý:

- Khi hai đường thẳng a, b vuông góc với nhau thì ta kí hiệu \(a \bot b\).

- Trong không gian, hai đường thẳng vuông góc với nhau thì hoặc cắt nhau, hoặc chéo nhau.

B. Bài tập

Bài 1: Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình vuông. Tính góc giữa các cặp đường thẳng sau:

a) A’B’ và BC.

b) A’D’ và BD.

c) B’C’ và AD.

Giải:

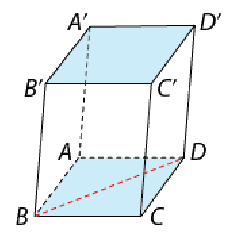
a) Ta có A’B’ // AB, suy ra (A’B’, BC) = (AB, BC).

Mà ABCD là hình vuông nên \(\widehat {ABC} = {90^o}\). Vậy \((A'B',BC) = {90^o}\).

b) Ta có A’D’ // AD, suy ra (A’D’, BD) = (AB, BD).

Mà ABCD là hình vuông nên \(\widehat {ADB} = {45^o}\). Vậy \((A'D',BD) = {45^o}\).

c) Ta có B’C’ // BC và BC // AD nên B’C’ // AD. Vậy \((B'C',AD) = {0^o}\).

Bài 2: Cho tứ diện đều ABCD có cạnh bằng a. Gọi E, F, M, K lần lượt là trung điểm của AB, CD, AC và AD. Chứng minh rằng \(EF \bot MK\).

Giải:

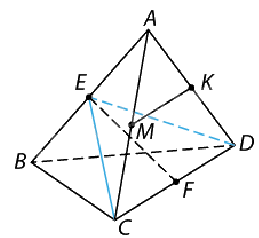
Lý thuyết Hai đường thẳng vuông góc - SGK Toán 11 Cùng khám phá 2

Ta có M và K lần lượt là trung điểm của AC và AD, do đó MK // CD.

Suy ra, góc giữa EF và MN bằng góc giữa EF và CD.

Do ABCD là tứ diện đều cạnh a nên các tam giác ABC và ABD là các tam giác đều cạnh a.

CE và DE là đường trung tuyến đồng thời là đường cao của các tam giác đều cạnh a. Ta tính được \(CE = DE = \frac{{\sqrt 3 }}{2}a\). Vậy tam giác CED cân tại E.

Do F là trung điểm cạnh đáy CD của tam giác cân CED nên \(EF \bot CD\).

Suy ra \((EF,MK) = (EF,CD) = {90^o}\).

Vậy \(EF \bot MK\).

Lý thuyết Hai đường thẳng vuông góc - SGK Toán 11 Cùng khám phá 3

Lý Thuyết Hai Đường Thẳng Vuông Góc - SGK Toán 11: Giải Thích Chi Tiết và Bài Tập Vận Dụng

Chào mừng các em học sinh đến với bài học về Lý thuyết Hai Đường Thẳng Vuông Góc trong chương trình SGK Toán 11. Đây là một chủ đề quan trọng, nền tảng cho nhiều kiến thức hình học nâng cao hơn. Tusach.vn sẽ cùng các em khám phá một cách chi tiết và dễ hiểu nhất.

1. Điều Kiện Hai Đường Thẳng Vuông Góc

Hai đường thẳng (Δ₁) và (Δ₂) được gọi là vuông góc với nhau khi và chỉ khi tích vô hướng của hai vectơ chỉ phương của chúng bằng 0. Cụ thể:

Nếu (Δ₁) có vectơ chỉ phương a = (a₁; a₂) và (Δ₂) có vectơ chỉ phương b = (b₁; b₂) thì (Δ₁) ⊥ (Δ₂) ⇔ a.b = a₁b₁ + a₂b₂ = 0.
Hoặc, nếu (Δ₁) có vectơ pháp tuyến n₁ = (a; b) và (Δ₂) có vectơ pháp tuyến n₂ = (c; d) thì (Δ₁) ⊥ (Δ₂) ⇔ n₁.n₂ = ac + bd = 0.

2. Quan Hệ Giữa Vectơ Chỉ Phương và Vectơ Pháp Tuyến của Hai Đường Thẳng Vuông Góc

Nếu hai đường thẳng (Δ₁) và (Δ₂) vuông góc với nhau, thì:

Vectơ chỉ phương của (Δ₁) vuông góc với vectơ pháp tuyến của (Δ₂).
Vectơ chỉ phương của (Δ₂) vuông góc với vectơ pháp tuyến của (Δ₁).

Điều này có nghĩa là, nếu chúng ta biết vectơ chỉ phương của một đường thẳng, chúng ta có thể dễ dàng tìm được vectơ pháp tuyến của đường thẳng vuông góc với nó.

3. Phương Trình Đường Thẳng Vuông Góc

Để tìm phương trình đường thẳng (Δ₂) vuông góc với đường thẳng (Δ₁) tại một điểm M(x₀; y₀), ta thực hiện các bước sau:

Tìm vectơ chỉ phương a của (Δ₁).
Tìm vectơ pháp tuyến n của (Δ₂) sao cho n vuông góc với a (tức là n.a = 0).
Sử dụng công thức phương trình đường thẳng đi qua điểm M(x₀; y₀) và có vectơ pháp tuyến n = (a; b): a(x - x₀) + b(y - y₀) = 0.

4. Bài Tập Vận Dụng

Bài 1: Cho đường thẳng d: 2x - y + 3 = 0. Viết phương trình đường thẳng Δ vuông góc với d và đi qua điểm A(1; 2).

Giải:

Vectơ pháp tuyến của d là n = (2; -1).
Vectơ chỉ phương của Δ là a = (1; 2).
Phương trình Δ: 1(x - 1) + 2(y - 2) = 0 ⇔ x + 2y - 5 = 0.

5. Lưu Ý Quan Trọng

Khi làm bài tập về hai đường thẳng vuông góc, các em cần chú ý:

Phân biệt rõ vectơ chỉ phương và vectơ pháp tuyến.
Sử dụng đúng công thức tích vô hướng để kiểm tra điều kiện vuông góc.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Hai Đường Thẳng Vuông Góc - SGK Toán 11. Chúc các em học tập tốt và đạt kết quả cao!

Để luyện tập thêm, các em có thể tham khảo các bài tập khác tại tusach.vn.