Bài 6.12 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 6.12 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Bài 6.12 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về phép biến hình để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho a, b, c là các số thực dương và khác 1. So sánh a, b, c và 1 trong mỗi trường hợp sau:
Đề bài
Cho a, b, c là các số thực dương và khác 1. So sánh a, b, c và 1 trong mỗi trường hợp sau:
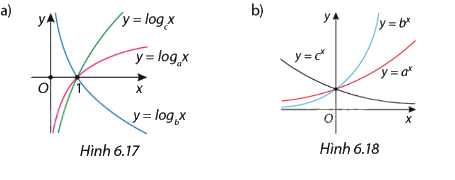
Phương pháp giải - Xem chi tiết
a) Hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) khi 0 < a < 1.
b) Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1.
Lời giải chi tiết
a) Ta thấy hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) nên a > 1
Ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) 0 < b < 1
Ta thấy hàm số \(y = {\log _c}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) c > 1
b) Ta thấy hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) nên a > 1
Ta thấy hàm số \(y = {b^x}\) đồng biến trên \(\mathbb{R}\) nên b > 1
Ta thấy hàm số \(y = {c^x}\) nghịch biến trên \(\mathbb{R}\) nên 0 < c < 1
Bài 6.12 Trang 19 SGK Toán 11 Tập 2 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 6.12 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về phép biến hình và ứng dụng vào giải quyết các bài toán hình học. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 6.12 yêu cầu học sinh thực hiện các phép biến hình trên một hình cho trước, xác định ảnh của các điểm và đường thẳng sau khi thực hiện phép biến hình. Bài tập thường yêu cầu sử dụng các phép tịnh tiến, quay, đối xứng trục và đối xứng tâm.
Lời giải chi tiết
Để giải bài 6.12, học sinh cần nắm vững các kiến thức sau:
- Phép tịnh tiến: Biến mỗi điểm M thành điểm M' sao cho vector MM' = v (v là vector tịnh tiến).
- Phép quay: Biến mỗi điểm M thành điểm M' sao cho góc giữa MM' và trục quay là α (α là góc quay).
- Phép đối xứng trục: Biến mỗi điểm M thành điểm M' sao cho trục đối xứng là đường trung trực của đoạn MM'.
- Phép đối xứng tâm: Biến mỗi điểm M thành điểm M' sao cho tâm đối xứng là trung điểm của đoạn MM'.
Ví dụ, giả sử bài tập yêu cầu thực hiện phép tịnh tiến theo vector v = (2, -1) lên điểm A(1, 3). Khi đó, điểm A' có tọa độ là (1+2, 3-1) = (3, 2).
Hướng dẫn giải bài tập
- Xác định phép biến hình: Đọc kỹ đề bài để xác định loại phép biến hình cần thực hiện (tịnh tiến, quay, đối xứng trục, đối xứng tâm).
- Xác định các yếu tố của phép biến hình: Xác định vector tịnh tiến, tâm quay, trục đối xứng, tâm đối xứng.
- Áp dụng công thức: Sử dụng công thức của từng phép biến hình để tính tọa độ điểm ảnh sau khi thực hiện phép biến hình.
- Kiểm tra lại kết quả: Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự
Để luyện tập thêm, học sinh có thể giải các bài tập tương tự trong SGK Toán 11 tập 2 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Lưu ý quan trọng
Khi giải bài tập về phép biến hình, học sinh cần chú ý đến các yếu tố sau:
- Đơn vị đo lường: Đảm bảo sử dụng cùng một đơn vị đo lường cho tất cả các đại lượng.
- Chiều của vector: Chú ý đến chiều của vector tịnh tiến và góc quay.
- Thứ tự thực hiện phép biến hình: Nếu thực hiện nhiều phép biến hình liên tiếp, cần chú ý đến thứ tự thực hiện.
Kết luận: Bài 6.12 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt môn Toán tại tusach.vn!
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | M'(x', y') = M(x+a, y+b) |
| Quay | (Công thức phức tạp hơn, tùy thuộc vào tâm quay và góc quay) |