Bài 9.10 trang 101 SGK Toán 11 tập 2
Bài 9.10 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải các bài toán hình học không gian cơ bản.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
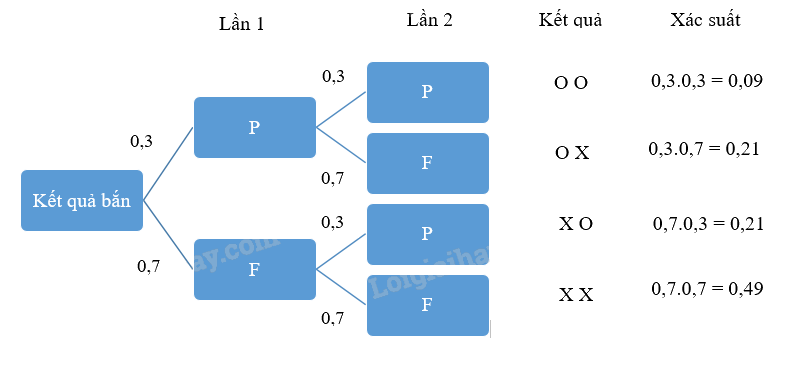
Xác suất bắn trúng bia của một người bắn cung là 0,3.
Bài 9.10 Trang 101 SGK Toán 11 Tập 2: Giải Chi Tiết và Phương Pháp
Bài 9.10 trang 101 SGK Toán 11 tập 2 là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đường thẳng và mặt phẳng trong không gian. Bài toán này thường yêu cầu học sinh xác định mối quan hệ giữa đường thẳng và mặt phẳng, tìm giao điểm, hoặc chứng minh tính song song, vuông góc.
Nội dung bài toán
Thông thường, bài 9.10 sẽ đưa ra một hình chóp hoặc một hình đa diện khác, và yêu cầu học sinh chứng minh một mối quan hệ nào đó giữa các đường thẳng và mặt phẳng trong hình đó. Ví dụ, chứng minh một đường thẳng song song với một mặt phẳng, hoặc chứng minh hai mặt phẳng vuông góc với nhau.
Phương pháp giải
Để giải bài 9.10 trang 101 SGK Toán 11 tập 2 hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa về đường thẳng song song với mặt phẳng: Một đường thẳng được gọi là song song với một mặt phẳng nếu nó không có điểm chung với mặt phẳng đó.
- Định nghĩa về đường thẳng vuông góc với mặt phẳng: Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
- Các dấu hiệu nhận biết đường thẳng song song với mặt phẳng:
- Nếu đường thẳng song song với một đường thẳng nằm trong mặt phẳng thì nó song song với mặt phẳng đó.
- Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia.
- Các dấu hiệu nhận biết đường thẳng vuông góc với mặt phẳng:
- Nếu đường thẳng vuông góc với một đường thẳng nằm trong mặt phẳng thì nó vuông góc với mặt phẳng đó.
- Nếu đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng thì nó vuông góc với mặt phẳng đó.
Ví dụ minh họa
Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng SM song song với mặt phẳng (ABCD).
Giải:
- Gọi N là trung điểm của AB. Ta có MN là đường trung bình của hình vuông ABCD, do đó MN song song với AD và BC.
- Vì ABCD là hình vuông, nên AD song song với BC.
- Xét mặt phẳng (SMN). Vì SM và MN không cùng nằm trong mặt phẳng (ABCD), nên mặt phẳng (SMN) cắt mặt phẳng (ABCD) theo đường thẳng MN.
- Do MN song song với AD và BC, nên MN song song với mặt phẳng (ABCD).
- Vậy SM song song với mặt phẳng (ABCD).
Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài toán, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, việc tìm hiểu các phương pháp giải toán hình học không gian trên các trang web như tusach.vn cũng rất hữu ích.
Lời khuyên
Khi giải bài toán về đường thẳng và mặt phẳng, học sinh nên vẽ hình chính xác và rõ ràng. Điều này sẽ giúp học sinh dễ dàng hình dung được mối quan hệ giữa các yếu tố trong bài toán và tìm ra phương pháp giải phù hợp. Đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn.
Chúc các em học tốt môn Toán 11!