Lý thuyết Logarit - SGK Toán 11 Cùng khám phá
Tổng quan nội dung
Lý thuyết Logarit - Nền tảng Toán học 11
Chào mừng bạn đến với chuyên mục Lý thuyết Logarit - SGK Toán 11 của tusach.vn! Logarit là một khái niệm quan trọng trong toán học, đóng vai trò then chốt trong nhiều lĩnh vực như giải phương trình, tính toán khoa học và phân tích dữ liệu.
Ở bài viết này, chúng tôi sẽ cung cấp một cách đầy đủ và dễ hiểu nhất về lý thuyết logarit, bao gồm định nghĩa, tính chất, các dạng bài tập thường gặp và hướng dẫn giải chi tiết.
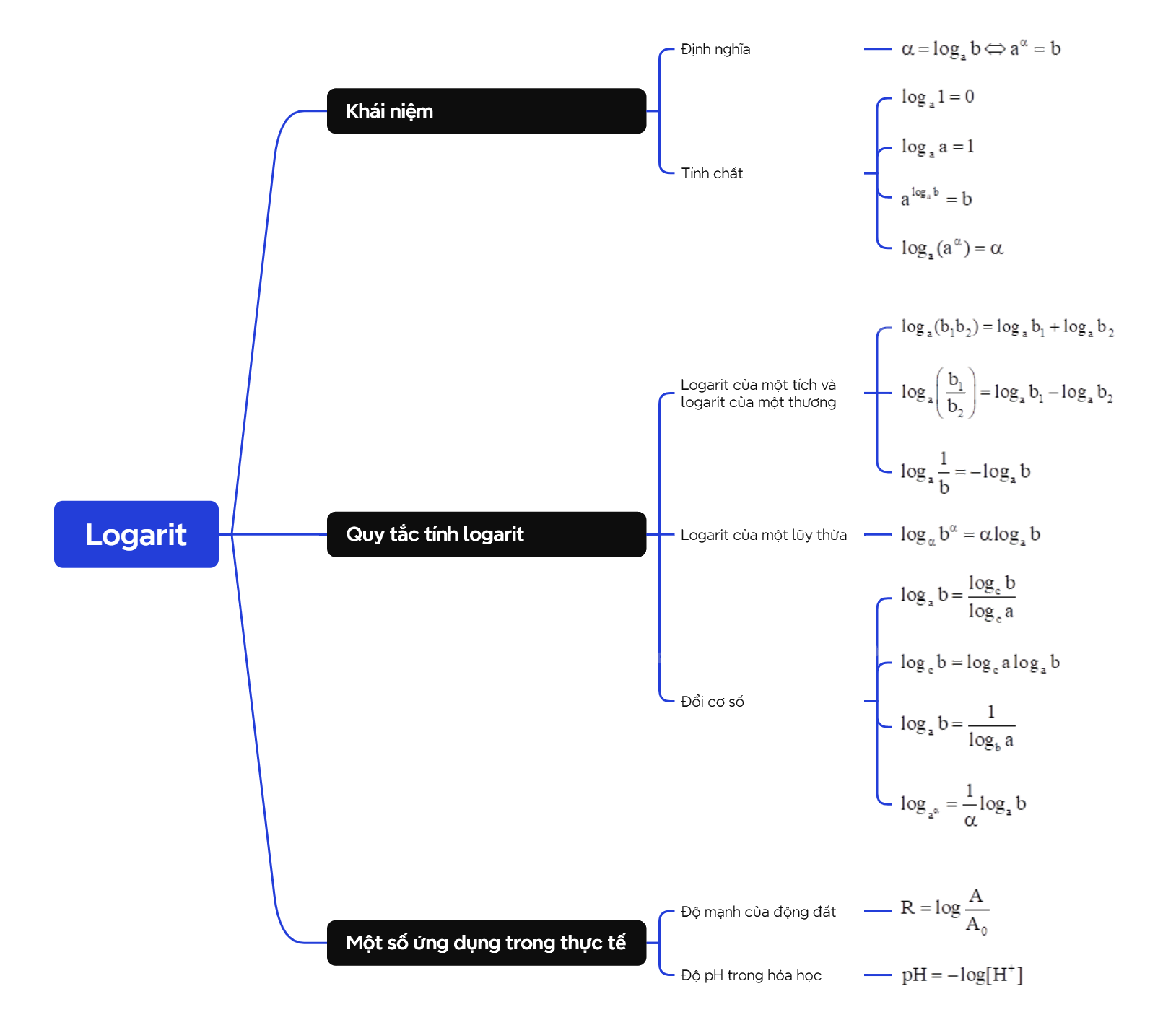
A. Lý thuyết 1. Khái niệm logarit a) Định nghĩa
A. Lý thuyết
1. Khái niệm logarit
a) Định nghĩa
Cho hai số thực dương a, b và a khác 1. Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là logarit cơ số a của b, kí hiệu \({\log _a}b\), nghĩa là \(\alpha = {\log _a}b \Leftrightarrow {a^\alpha } = b\). |
Lưu ý:
- Không tồn tại logarit của số âm và số 0.
- Logarit cơ số 10 của một số dương b là logarit thập phân của b, ký hiệu logb hay lgb.
- Logarit cơ số e của một số dương b là logarit tự nhiên (hay logarit Nê-pe) của b, ký hiệu lnb.
b) Tính chất
Cho a là một số dương khác 1, b là một số dương và số thực \(\alpha \). +) \({\log _a}1 = 0\) +) \({\log _a}a = 1\) +) \({a^{{{\log }_a}b}} = b\) +) \({\log _a}({a^\alpha }) = \alpha \) |
2. Quy tắc tính logarit
a) Logarit của một tích và logarit của một thương
Cho ba số dương a, \({b_1}\), \({b_2}\) và \(a \ne 1\). Khi đó: +) \({\log _a}({b_1}{b_2}) = {\log _a}{b_1} + {\log _a}{b_2}\) +) \({\log _a}\left( {\frac{{{b_1}}}{{{b_2}}}} \right) = {\log _a}{b_1} - {\log _a}{b_2}\) |
Lưu ý: \({\log _a}\frac{1}{b} = - {\log _a}b\).
b) Logarit của một lũy thừa
Cho hai số dương a, b với \(a \ne 1\). Với mọi \(\alpha \), ta có: \({\log _\alpha }{b^\alpha } = \alpha {\log _a}b\). |
Lưu ý : \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\) \((n \in \mathbb{N},n \ge 2)\).
c) Đổi cơ số
Cho ba số thực dương a, b, c với \(a \ne 1\). Khi đó: \({\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\) hay \({\log _c}b = {\log _c}a{\log _a}b\). |
Lưu ý:
- Với a, b là hai số thực dương khác 1, ta có \({\log _a}b = \frac{1}{{{{\log }_b}a}}\) hay \({\log _a}b.{\log _b}a = 1\).
- Với a là một số dương khác 1, b là số thực dương và \(\alpha \ne 0\), ta có \({\log _{{a^\alpha }}} = \frac{1}{\alpha }{\log _a}b\).
3. Một số ứng dụng trong thực tế
a) Độ mạnh của động đất
\(R = \log \frac{A}{{{A_0}}}\) (độ Richter).
b) Độ pH trong hóa học
\(pH = - \log [{H^ + }]\).
B. Bài tập
Bài 1: Tính:
a) \({\log _2}8\).
b) \({\log _{\frac{1}{2}}}4\).
c) \({\log _3}\frac{1}{{27}}\).
Giải:
a) \({\log _2}8 = 3\) vì \({2^3} = 8\).
b) \({\log _{\frac{1}{2}}}4 = - 2\) vì \({\left( {\frac{1}{2}} \right)^{ - 2}} = 4\).
c) \({\log _3}\frac{1}{{27}} = - 3\) vì \({3^{ - 3}} = \frac{1}{{27}}\).
Bài 2: Tính:
a) \({3^{2{{\log }_3}5}}\).
b) \({\log _{\frac{1}{2}}}\sqrt {\frac{1}{8}} \).
Giải:
a) \({3^{2{{\log }_3}5}} = {({3^{{{\log }_3}5}})^2} = {5^2} = 25\).
b) \({\log _{\frac{1}{2}}}\sqrt {\frac{1}{8}} = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^{\frac{3}{2}}} = \frac{3}{2}\).
Bài 3: Không sử dụng máy tính cầm tay, tính các giá trị biểu thức sau:
a) \(A = {\log _6}3 + {\log _6}12\).
b) \(B = {\log _7}21 - {\log _7}147\).
Giải:
a) \(A = {\log _6}3 + {\log _6}12 = {\log _6}(3.12) = {\log _6}(36) = 2\).
b) \(B = {\log _7}21 - {\log _7}147 = {\log _7}\frac{{21}}{{147}} = {\log _7}\frac{1}{7} = {\log _7}{7^{ - 1}} = - 1\).
Bài 4: Cho \(a = {\log _3}x\); \(b = {\log _3}y\); \(c = {\log _3}z\). Tính \({\log _3}\left( {\frac{{\sqrt[3]{x}}}{{{y^2}.{z^4}}}} \right)\) theo a, b, c.
Giải:
\({\log _3}\left( {\frac{{\sqrt[3]{x}}}{{{y^2}.{z^4}}}} \right) = {\log _3}\sqrt[3]{x} - ({\log _3}{y^2} + {\log _3}{z^4}) = \frac{1}{3}{\log _3}x - (2{\log _3}y + 4{\log _3}z) = \frac{1}{3}a - 2b - 4c\).
Bài 5:
a) Không sử dụng máy tính cầm tay, tính giá trị biểu thức \({\log _{\frac{1}{4}}}({\log _3}4.{\log _2}3)\).
b) Cho \(\alpha = {\log _3}45\). Tính \({\log _{45}}5\) theo a.
Giải:
a) \({\log _{\frac{1}{4}}}({\log _3}4.{\log _2}3) = {\log _{\frac{1}{4}}}(2{\log _3}2.{\log _2}3) = {\log _{\frac{1}{4}}}2 = {\log _{{2^{ - 2}}}}2 = - \frac{1}{2}\).
b) Ta có \(\alpha = {\log _3}45 = {\log _3}({3^2}.5) = 2{\log _3}3 + {\log _3}5 = 2 + {\log _3}5\).
Suy ra \({\log _3}5 = \alpha - 2\). Vậy \({\log _{45}}5 = \frac{{{{\log }_3}5}}{{{{\log }_3}45}} = \frac{{\alpha - 2}}{\alpha }\).
Lý Thuyết Logarit - SGK Toán 11: Tổng Quan Chi Tiết
Logarit là một khái niệm quan trọng trong chương trình Toán 11, thường gây khó khăn cho học sinh. Bài viết này sẽ giúp bạn nắm vững kiến thức nền tảng và kỹ năng giải bài tập liên quan đến logarit.
1. Định Nghĩa Logarit
Logarit của một số dương b theo cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: logab = x.
- a: Cơ số của logarit.
- b: Số bị logarit (luôn dương).
- x: Giá trị logarit.
2. Các Tính Chất Quan Trọng của Logarit
- Logarit của tích: loga(xy) = logax + logay
- Logarit của thương: loga(x/y) = logax - logay
- Logarit của lũy thừa: loga(xn) = n.logax
- Đổi cơ số logarit: logab = logcb / logca
- Logarit cơ số 10: log10x được ký hiệu là log x
- Logarit tự nhiên: logex được ký hiệu là ln x (e ≈ 2.718)
3. Các Dạng Bài Tập Logarit Thường Gặp
Dưới đây là một số dạng bài tập logarit thường gặp trong SGK Toán 11:
- Tính giá trị biểu thức logarit: Sử dụng định nghĩa và các tính chất logarit để tính giá trị của biểu thức.
- Giải phương trình logarit: Chuyển phương trình về dạng cơ bản và sử dụng các tính chất logarit để giải.
- Giải bất phương trình logarit: Tương tự như giải phương trình, nhưng cần chú ý đến điều kiện xác định và chiều bất đẳng thức.
- Sử dụng logarit để tính toán: Áp dụng logarit để đơn giản hóa các phép tính phức tạp.
4. Ví Dụ Minh Họa
Ví dụ 1: Tính log28.
Giải: Vì 23 = 8, nên log28 = 3.
Ví dụ 2: Giải phương trình log3(x + 2) = 2.
Giải: x + 2 = 32 => x + 2 = 9 => x = 7.
5. Lưu Ý Quan Trọng
- Luôn kiểm tra điều kiện xác định của logarit (số bị logarit phải dương, cơ số phải dương và khác 1).
- Sử dụng các tính chất logarit một cách linh hoạt để đơn giản hóa bài toán.
- Luyện tập thường xuyên để nắm vững kỹ năng giải bài tập.
6. Bảng Công Thức Logarit Quan Trọng
| Công Thức | Mô Tả |
|---|---|
| loga(xy) = logax + logay | Logarit của tích |
| loga(x/y) = logax - logay | Logarit của thương |
| loga(xn) = n.logax | Logarit của lũy thừa |
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Logarit - SGK Toán 11. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất trong các kỳ thi!
Truy cập tusach.vn để xem thêm nhiều tài liệu học tập và bài tập luyện thi Toán 11.