Bài 8.9 trang 63 SGK Toán 11 tập 2

Bài 8.9 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm của hàm số.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

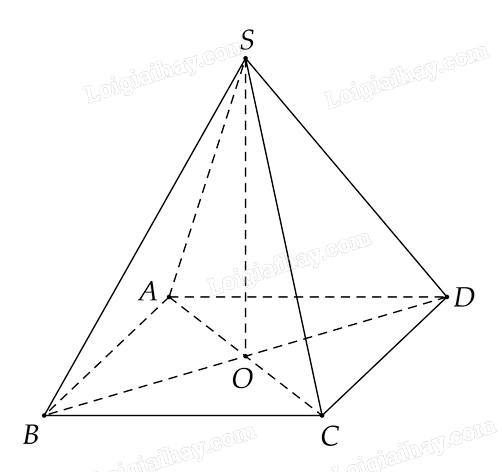
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD.

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD. Chứng minh \(BC \bot SO\) và \(SC \bot BD\).

Phương pháp giải - Xem chi tiết Bài 8.9 trang 63 SGK Toán 11 tập 2 - Cùng khám phá 1

Chứng minh \(SO \bot AC,SO \bot BD\) từ đó suy ra \(SO \bot \left( {ABCD} \right)\) và suy ra \(SO \bot BC\)

Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot SC\)

Lời giải chi tiết

Bài 8.9 trang 63 SGK Toán 11 tập 2 - Cùng khám phá 2

+) Vì \(ABCD\) là hình thoi nên \(AC \bot BD\) tại trung điểm \(O\) của mỗi đường

Vì \(SA = SC \Rightarrow \Delta SAC\) cân tại \(S\) và \(O\) là trung điểm \(AC\) nên \(SO \bot AC\)

Vì \(SB = SD\)\( \Rightarrow \Delta SBD\) cân tại \(S\) và \(O\) là trung điểm \(BD\) nên \(SO \bot BD\)

Ta có \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BC\)

+) Vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BD\)

Ta có \(\left\{ \begin{array}{l}SO \bot BD\\AC \bot BD\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)

Bài 8.9 trang 63 SGK Toán 11 tập 2: Giải chi tiết và hướng dẫn

Bài 8.9 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập:

Cho hàm số f(x) = x³ - 3x² + 2. Tính f'(x) và tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm f'(x):

Sử dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:

f'(x) = 3x² - 6x

Tìm các điểm cực trị:

Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2

Xác định loại cực trị:

Ta xét dấu của f'(x) trên các khoảng:

Khoảng (-∞, 0): Chọn x = -1, f'(-1) = 3(-1)² - 6(-1) = 9 > 0, hàm số đồng biến.
Khoảng (0, 2): Chọn x = 1, f'(1) = 3(1)² - 6(1) = -3 < 0, hàm số nghịch biến.
Khoảng (2, +∞): Chọn x = 3, f'(3) = 3(3)² - 6(3) = 9 > 0, hàm số đồng biến.

Vậy:

Tại x = 0, hàm số đạt cực đại, giá trị cực đại là f(0) = 2.
Tại x = 2, hàm số đạt cực tiểu, giá trị cực tiểu là f(2) = 2³ - 3(2)² + 2 = -2.

Kết luận:

Hàm số f(x) = x³ - 3x² + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.

Mở rộng và bài tập tương tự

Để hiểu sâu hơn về ứng dụng của đạo hàm trong việc tìm cực trị của hàm số, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 11 tập 2 và các tài liệu ôn tập khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.

Ví dụ bài tập tương tự:

Cho hàm số g(x) = -x³ + 3x² - 1. Tìm các điểm cực trị của hàm số.

Lưu ý:

Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
Sử dụng đúng các quy tắc đạo hàm để tránh sai sót.
Phân tích kỹ dấu của đạo hàm để xác định đúng loại cực trị.

Chúc bạn học tốt!

Bài 8.9 trang 63 SGK Toán 11 tập 2 - Cùng khám phá