Bài 1.14 trang 19 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 1.14 trang 19 SGK Toán 11 tập 1 - Cùng khám phá
Bài 1.14 thuộc chương trình Toán 11 tập 1, tập trung vào việc nghiên cứu hàm số bậc hai và đồ thị parabol. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa, tính chất của hàm số bậc hai để xác định các yếu tố của parabol và vẽ đồ thị.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.
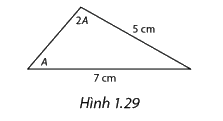
Cho tam giác có số đo các góc như Hình 1.29. Tính (cos A).
Đề bài
Cho tam giác có số đo các góc như Hình 1.29. Tính \(\cos A\).
Phương pháp giải - Xem chi tiết
Áp dụng định lý Sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) (a, b, c lần lượt là cạnh đối diện với góc A, B, C trong tam giác)
Lời giải chi tiết
\(\begin{array}{l}\frac{5}{{\sin A}} = \frac{7}{{\sin 2A}}\\ \Leftrightarrow 5\sin 2A = 7\sin A\\ \Leftrightarrow 10\sin A\cos A = 7\sin A\\ \Leftrightarrow \cos A = \frac{7}{{10}}\end{array}\)
Bài 1.14 trang 19 SGK Toán 11 tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 1.14 trang 19 SGK Toán 11 tập 1 yêu cầu chúng ta xét hàm số y = f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
- Xác định các hệ số a, b, c.
- Xác định đỉnh của parabol.
- Xác định trục đối xứng của parabol.
- Tìm giao điểm của parabol với trục hoành.
- Tìm giao điểm của parabol với trục tung.
- Vẽ đồ thị của hàm số.
Giải chi tiết
1. Xác định các hệ số a, b, c:
Hàm số y = f(x) = x2 - 4x + 3 có các hệ số:
- a = 1
- b = -4
- c = 3
2. Xác định đỉnh của parabol:
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2
Tung độ đỉnh của parabol là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1
Vậy, đỉnh của parabol là I(2; -1).
3. Xác định trục đối xứng của parabol:
Trục đối xứng của parabol là đường thẳng x = x0 = x = 2.
4. Tìm giao điểm của parabol với trục hoành:
Giao điểm của parabol với trục hoành là nghiệm của phương trình f(x) = 0:
x2 - 4x + 3 = 0
Giải phương trình bậc hai, ta được:
Δ = b2 - 4ac = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4
x1 = (-b + √Δ) / (2a) = (4 + 2) / 2 = 3
x2 = (-b - √Δ) / (2a) = (4 - 2) / 2 = 1
Vậy, parabol cắt trục hoành tại hai điểm A(1; 0) và B(3; 0).
5. Tìm giao điểm của parabol với trục tung:
Giao điểm của parabol với trục tung là điểm có hoành độ x = 0:
y = f(0) = 02 - 4 * 0 + 3 = 3
Vậy, parabol cắt trục tung tại điểm C(0; 3).
6. Vẽ đồ thị của hàm số:
Dựa vào các thông tin đã tính toán, ta có thể vẽ đồ thị của hàm số y = x2 - 4x + 3:
- Đỉnh I(2; -1)
- Trục đối xứng x = 2
- Giao điểm với trục hoành A(1; 0) và B(3; 0)
- Giao điểm với trục tung C(0; 3)
Lưu ý quan trọng
Khi vẽ đồ thị, cần chú ý đến hệ số a. Vì a = 1 > 0, parabol có dạng mở lên trên.
Việc xác định chính xác các yếu tố của parabol (đỉnh, trục đối xứng, giao điểm) là rất quan trọng để vẽ đồ thị chính xác.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 1 và các tài liệu tham khảo khác.
tusach.vn hy vọng với lời giải chi tiết này, bạn sẽ hiểu rõ hơn về Bài 1.14 trang 19 SGK Toán 11 tập 1 và tự tin giải các bài tập tương tự.