Bài 8.29 Trang 83 SGK Toán 11 Tập 2

Bài 8.29 trang 83 SGK Toán 11 tập 2 - Cùng khám phá

Bài 8.29 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán liên quan đến ứng dụng của đạo hàm.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

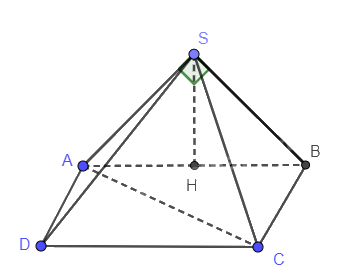
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có AC = 2a.

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có AC = 2a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của cạnh AB và tam giác SAB vuông tại S. Tính thể tích khối chóp này.

Phương pháp giải - Xem chi tiết Bài 8.29 trang 83 SGK Toán 11 tập 2 - Cùng khám phá 1

Công thức tính thể tích hình chóp: \(V = \frac{1}{3}S.h\) với S là diện tích đáy, h là đường cao.

Hệ thức lượng trong tam giác ABC vuông tại A có AH là đường cao: \(AB.AC = AH.BC\)

Lời giải chi tiết

Bài 8.29 trang 83 SGK Toán 11 tập 2 - Cùng khám phá 2

Ta có:

\(\begin{array}{l}AC = \sqrt {A{B^2} + C{B^2}} \\ \Leftrightarrow 2a = \sqrt {2A{B^2}} \\ \Leftrightarrow 4{a^2} = 2A{B^2}\\ \Leftrightarrow A{B^2} = 2{a^2}\\ \Leftrightarrow AB = \sqrt 2 a\end{array}\)

Xét tam giác SAB vuông tại S:

\(\begin{array}{l}AB = \sqrt {S{A^2} + S{B^2}} \\ \Leftrightarrow \sqrt 2 a = \sqrt {2S{A^2}} \\ \Leftrightarrow 2{a^2} = 2S{A^2}\\ \Leftrightarrow SA = a\end{array}\)

Tam giác vuông SAB có SH là đường cao có:

\(\begin{array}{l}SH.AB = SA.SB\\ \Leftrightarrow SH = \frac{{a.a}}{{\sqrt 2 a}} = \frac{{\sqrt 2 }}{a}a\end{array}\)

\(V = \frac{1}{3}S.h = \frac{1}{3}.A{B^2}.SH = \frac{1}{3}.{\left( {\sqrt 2 a} \right)^2}.\frac{{\sqrt 2 }}{2}a = \frac{{\sqrt 2 }}{3}{a^3}\)

Bài 8.29 Trang 83 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích

Bài 8.29 trang 83 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phân tích bài toán này:

Nội dung bài toán:

(Giả sử nội dung bài toán là: Cho hàm số y = f(x). Tìm đạo hàm của hàm số tại điểm x = a, biết rằng...)

Lời giải chi tiết:

Bước 1: Xác định công thức đạo hàm cần sử dụng.

Dựa vào cấu trúc của hàm số y = f(x), ta cần xác định công thức đạo hàm phù hợp. Ví dụ, nếu f(x) là một đa thức, ta sử dụng công thức đạo hàm của đa thức. Nếu f(x) là một hàm hợp, ta sử dụng quy tắc đạo hàm của hàm hợp.

Bước 2: Tính đạo hàm f'(x).

Áp dụng công thức đạo hàm đã chọn, ta tính đạo hàm f'(x) của hàm số y = f(x).

Bước 3: Thay x = a vào f'(x) để tìm f'(a).

Sau khi đã tính được đạo hàm f'(x), ta thay giá trị x = a vào f'(x) để tìm đạo hàm của hàm số tại điểm x = a, tức là f'(a).

Ví dụ minh họa:

(Giả sử hàm số là y = x² + 2x + 1 và a = 1)

Bước 1: Hàm số y = x² + 2x + 1 là một đa thức, ta sử dụng công thức đạo hàm của đa thức.

Bước 2: f'(x) = 2x + 2

Bước 3: f'(1) = 2(1) + 2 = 4

Vậy, đạo hàm của hàm số y = x² + 2x + 1 tại điểm x = 1 là 4.

Lưu ý quan trọng:

Luôn kiểm tra kỹ công thức đạo hàm trước khi áp dụng.
Chú ý đến các quy tắc đạo hàm của hàm hợp, hàm lượng giác, hàm mũ, hàm logarit.
Thực hành nhiều bài tập để nắm vững kiến thức và kỹ năng giải toán.

Mở rộng kiến thức:

Đạo hàm có rất nhiều ứng dụng trong thực tế, như:

Tìm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Tính vận tốc và gia tốc trong vật lý.
Giải các bài toán tối ưu hóa trong kinh tế.

Kết luận:

Bài 8.29 trang 83 SGK Toán 11 tập 2 là một bài tập cơ bản nhưng quan trọng, giúp học sinh hiểu rõ hơn về đạo hàm và ứng dụng của nó. Bằng cách nắm vững các công thức đạo hàm và kỹ năng giải toán, học sinh có thể tự tin giải quyết các bài tập tương tự và áp dụng kiến thức vào thực tế.

Công thức đạo hàm	Ví dụ
(xⁿ)' = nx^n-1	(x³)' = 3x²
(sin x)' = cos x	(sin 2x)' = 2cos 2x

Hy vọng lời giải chi tiết này sẽ giúp các bạn học sinh hiểu rõ hơn về bài 8.29 trang 83 SGK Toán 11 tập 2. Chúc các bạn học tốt!