Giải mục 3 trang 47, 48, 49 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 47, 48, 49 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 47, 48, 49 sách giáo khoa Toán 11 tập 1. Bài viết này được tusach.vn biên soạn nhằm hỗ trợ các em trong quá trình tự học và ôn tập môn Toán.
Chúng tôi sẽ cung cấp các bước giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng để các em có thể nắm vững kiến thức và áp dụng vào các bài tập tương tự.
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
Hoạt động 6
Cho hai dãy số \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) mà \({u_n} = 1 + \frac{1}{n}\) và \({v_n} = 2 - \frac{1}{n}\) (n là số nguyên dương).
a) So sánh \({u_{n + 1}}\) và \({u_n}\).
b) So sánh \({v_{n + 1}}\) và \({v_n}\).
Phương pháp giải:
Thay n = n + 1 vào công thức tổng quát của dãy số. So sánh \({u_{n + 1}} - {u_n}\), \({v_{n + 1}} - {v_n}\) với 0.
Lời giải chi tiết:
a) Ta có: \({u_{n + 1}} - {u_n} = 1 + \frac{1}{{n + 1}} - 1 - \frac{1}{n} = \frac{1}{{n + 1}} - \frac{1}{n} = \frac{{n - \left( {n + 1} \right)}}{{n\left( {n + 1} \right)}} = \frac{ -1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{ -1}{{n\left( {n + 1} \right)}} < 0\)\( \Rightarrow {u_{n + 1}} - {u_n} < 0 \Rightarrow {u_{n + 1}} < {u_n}\).
b) Ta có: \({v_{n + 1}} - {v_n} = 2 - \frac{1}{{n + 1}} - 2 + \frac{1}{n} = \frac{1}{n} - \frac{1}{{n + 1}} = \frac{{n + 1 - n}}{{n\left( {n + 1} \right)}} = \frac{1}{{n\left( {n + 1} \right)}}\)
Mà n là số nguyên dương nên \(\frac{1}{{n\left( {n + 1} \right)}} > 0 \Rightarrow {v_{n + 1}} - {v_n} > 0 \Rightarrow {v_{n + 1}} > {v_n}\).
Luyện tập 5
Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) cho bởi \({u_n} = \frac{{n - 2}}{{3n - 1}},\forall n \in {\mathbb{N}^*}\) là một dãy số tăng.
Phương pháp giải:
So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
Lời giải chi tiết:
\(\begin{array}{l}{u_{n + 1}} = \frac{{n + 1 - 2}}{{3(n + 1) - 1}} = \frac{{n - 1}}{{3n + 2}}\\{u_{n + 1}} - {u_n} = \frac{{n - 1}}{{3n + 2}} - \frac{{n - 2}}{{3n - 1}} = \frac{5}{{9{n^2} + 3n - 2}}\\9{n^2} + 3n - 2 > 0\forall n \ge 1 \Rightarrow \frac{5}{{9{n^2} + 3n - 2}} > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0\end{array}\)
\(\Rightarrow {u_{n + 1}} > {u_n}\forall n\)
Vậy dãy số đã cho là một dãy số tăng.
Hoạt động 7
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\sqrt n }}{{n + 1}}\)
a) So sánh n + 1 và \(2\sqrt n \) .
b) Suy ra: \({u_n} \le \frac{1}{2}\), với mọi số nguyên dương n.
Phương pháp giải:
a) So sánh \(n + 1 - 2\sqrt n \) với 0.
b) Áp dụng phần a.
Lời giải chi tiết:
a) \(n + 1 - 2\sqrt n = {\left( {\sqrt n - 1} \right)^2} \ge 0\forall n \Rightarrow n + 1 \ge 2\sqrt n \)
b) \(n + 1 \ge 2\sqrt n \Rightarrow \frac{{\sqrt n }}{{n + 1}} \le \frac{{\sqrt n }}{{2\sqrt n }} = \frac{1}{2} \Rightarrow {u_n} = \frac{1}{2}\forall n\) nguyên dương
Luyện tập 6
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n - 1}}{{n + 2}}\), với n là số nguyên dương.
a) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) tăng.
b) Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) bị chặn.
Phương pháp giải:
a) So sánh \({u_{n + 1}}\) và \({u_n}\). Nếu \({u_{n + 1}} > {u_n}\forall n\) thì là dãy số tăng.
b) Dãy số \(\left( {{u_n}} \right)\) bị chặn khi \(m \le {u_n} \le M\forall n\) nguyên dương.
Lời giải chi tiết:
a)
\(\begin{array}{l}{u_n} = \frac{{n - 1}}{{n + 2}} = 1 - \frac{3}{{n + 2}}\\{u_{n + 1}} - {u_n} = 1 - \frac{3}{{n + 3}} - \left( {1 - \frac{3}{{n + 2}}} \right) = \frac{3}{{n + 2}} - \frac{3}{{n + 3}} = 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right)\\n + 2 < n + 3 \Rightarrow \frac{1}{{n + 2}} > \frac{1}{{n + 3}} \Leftrightarrow \frac{1}{{n + 2}} - \frac{1}{{n + 3}} > 0 \Leftrightarrow 3\left( {\frac{1}{{n + 2}} - \frac{1}{{n + 3}}} \right) > 0\\ \Rightarrow {u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\end{array}\)
Vậy dãy số đã cho là dãy số tăng.
b) n là số nguyên dương \( \Rightarrow n \ge 1 \Leftrightarrow \left\{ \begin{array}{l}n - 1 \ge 0\\n + 2 > 0\end{array} \right. \Leftrightarrow \frac{{n - 1}}{{n + 2}} \ge 0\)
\(n - 1 < n + 2 \Rightarrow \frac{{n - 1}}{{n + 2}} < 1\)
\( \Rightarrow 0 \le \frac{{n - 1}}{{n + 2}} < 1\forall n\) nguyên dương
Vậy dãy số đã cho là dãy số bị chặn.
Vận dụng
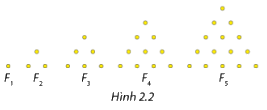
Trong một trò chơi của trẻ em, các em nhỏ dùng các viên bi để xếp thành các hình tam giác Fn. Dãy các hình xếp (Fn) tuân theo một quy luật được mô tả trong Hình 2.2. Trong đó F1 chỉ có 1 viên bi, thêm 2 viên bi để được tam giác đều là hình F2, thêm 3 viên bi thẳng hàng và song song với một cạnh của F2 để được tam giác đều F3,… Gọi (un) là dãy số mà un là số viên bi cần dùng để xếp được hình Fn \(\left( {n \in {\mathbb{N}^*}} \right)\). Chẳng hạn \({u_1} = 1,{u_2} = 3,{u_3} = 6\),…
a) Viết sáu số hạng đầu tiên của dãy số (un).
b) Dự đoán công thức truy hồi để tính un.
Phương pháp giải:
Số hạng đứng sau hơn số hạng đứng trước đúng một số bằng số thứ tự của số hạng đứng sau.
Lời giải chi tiết:
a) \({u_1} = 1,{u_2} = 3,{u_3} = 6,{u_4} = 6 + 4 = 10,{u_5} = 10 + 5 = 15,{u_6} = 15 + 6 = 21\)
b) Công tính truy hồi: \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + n + 1\end{array} \right.\)
Giải mục 3 trang 47, 48, 49 SGK Toán 11 tập 1: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 11 tập 1 thường xoay quanh các chủ đề về hàm số lượng giác, phương trình lượng giác, hoặc các bài toán liên quan đến vectơ. Việc nắm vững kiến thức nền tảng và phương pháp giải là vô cùng quan trọng để giải quyết các bài tập một cách hiệu quả.
Nội dung chính của Mục 3
- Các khái niệm cơ bản: Ôn lại các định nghĩa về hàm số lượng giác, tập xác định, tập giá trị, tính tuần hoàn.
- Các tính chất của hàm số lượng giác: Tìm hiểu về tính đơn điệu, tính chẵn lẻ, và các điểm cực trị của hàm số lượng giác.
- Phương trình lượng giác cơ bản: Giải các phương trình lượng giác đơn giản như sin(x) = a, cos(x) = a, tan(x) = a, cot(x) = a.
- Phương pháp giải phương trình lượng giác: Sử dụng các công thức lượng giác, biến đổi phương trình về dạng cơ bản, và giải bằng phương pháp đặt ẩn phụ.
Giải chi tiết các bài tập trang 47, 48, 49
Bài 1: (Trang 47)
(Giả sử đây là một bài tập về tìm tập xác định của hàm số lượng giác)
Để tìm tập xác định của hàm số y = f(x), ta cần xác định các giá trị của x sao cho biểu thức f(x) có nghĩa. Trong trường hợp hàm số lượng giác, ta cần chú ý đến mẫu số khác 0 và điều kiện của căn bậc hai (nếu có).
Ví dụ: Nếu hàm số là y = 1/sin(x), thì tập xác định là D = {x | x ≠ kπ, k ∈ Z}.
Bài 2: (Trang 48)
(Giả sử đây là một bài tập về xét tính chẵn lẻ của hàm số)
Để xét tính chẵn lẻ của hàm số y = f(x), ta cần kiểm tra hai điều kiện sau:
- f(-x) = f(x) (hàm số chẵn)
- f(-x) = -f(x) (hàm số lẻ)
Ví dụ: Hàm số y = cos(x) là hàm số chẵn vì cos(-x) = cos(x). Hàm số y = sin(x) là hàm số lẻ vì sin(-x) = -sin(x).
Bài 3: (Trang 49)
(Giả sử đây là một bài tập về giải phương trình lượng giác)
Để giải phương trình lượng giác, ta có thể sử dụng các công thức lượng giác cơ bản, biến đổi phương trình về dạng đơn giản, và giải bằng phương pháp đặt ẩn phụ. Ví dụ, để giải phương trình sin(x) = 1/2, ta có thể sử dụng công thức nghiệm của phương trình sin(x) = a.
Lưu ý khi giải bài tập Mục 3
- Nắm vững các định nghĩa và tính chất của hàm số lượng giác.
- Thành thạo các công thức lượng giác cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi giải bài tập.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập môn Toán 11. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!