Bài 8.12 trang 63 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.12 trang 63 SGK Toán 11 tập 2
Bài 8.12 thuộc chương trình Toán 11 tập 2, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến phép đếm và các quy tắc tổ hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy và \(SA = \sqrt 2 .a\).
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy và \(SA = \sqrt 2 .a\).Tính số đo góc giữa SC và (SAB)
Phương pháp giải - Xem chi tiết
Chứng minh \(BC \bot \left( {SAB} \right)\) từ đó suy ra \(SB\) là hình chiếu của \(SC\) trên \(\left( {SAB} \right)\)
Từ đó xác định góc cần tìm là góc \(\widehat {BSC}\)
Sử dụng Định lý Pi – ta – go để tính cạnh \(SB\) trong \(\Delta SAB\) vuông tại \(A\)
Sử dụng \(\tan \alpha \) để tính góc \(\widehat {BSC}\) trong tam giác \(SBC\) vuông tại \(B\)
Lời giải chi tiết
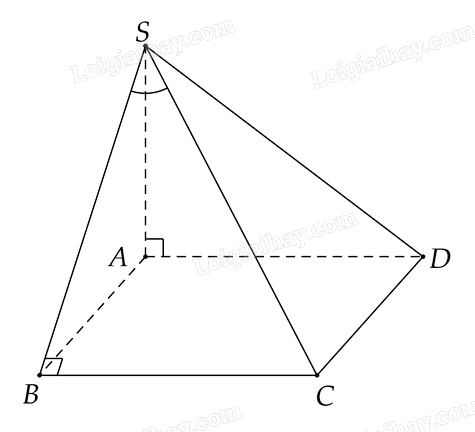
Ta có \(SA \bot BC\) vì \(SA \bot \left( {ABCD} \right)\)
Vì \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
Suy ra \(SB\) là hình chiếu vuông góc của \(SC\) trên \(\left( {SAB} \right)\)
Vậy góc giữa \(SC\) và \(\left( {SAB} \right)\) là góc giữa \(SC\) và \(SB\)
Vậy góc đó là góc \(\widehat {BSC}\)
Xét \(\Delta SAB\) vuông tại \(A\) có \(SA = a\sqrt 2 ,AB = a \Rightarrow SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Xét \(\Delta SBC\) vuông tại \(B\) có \(\tan \widehat {BSC} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {BSC} = {30^o}\)
Bài 8.12 Trang 63 SGK Toán 11 Tập 2: Giải Chi Tiết và Hướng Dẫn
Bài 8.12 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về tổ hợp và xác suất. Bài tập này thường yêu cầu học sinh tính số lượng các kết quả có thể xảy ra trong một thí nghiệm hoặc tình huống cụ thể.
Nội dung bài tập 8.12 trang 63 SGK Toán 11 tập 2
Bài tập thường có dạng như sau: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng từ hộp. Tính xác suất để:
- a) Cả hai quả bóng đều màu đỏ.
- b) Có ít nhất một quả bóng màu xanh.
- c) Hai quả bóng khác màu.
Phương pháp giải bài tập 8.12 trang 63 SGK Toán 11 tập 2
Để giải bài tập này, chúng ta cần sử dụng các công thức và quy tắc sau:
- Quy tắc cộng: Nếu một sự kiện A có thể xảy ra theo m cách, và một sự kiện B có thể xảy ra theo n cách, thì số cách để xảy ra một trong hai sự kiện A hoặc B là m + n.
- Quy tắc nhân: Nếu một sự kiện A có thể xảy ra theo m cách, và sau khi sự kiện A xảy ra, sự kiện B có thể xảy ra theo n cách, thì số cách để cả hai sự kiện A và B xảy ra là m * n.
- Hoán vị: Số hoán vị của n phần tử là n! (n giai thừa).
- Tổ hợp: Số tổ hợp chập k của n phần tử là C(n, k) = n! / (k! * (n-k)!).
- Xác suất: P(A) = Số kết quả thuận lợi cho A / Tổng số kết quả có thể xảy ra.
Lời giải chi tiết bài tập 8.12 trang 63 SGK Toán 11 tập 2
a) Tính xác suất để cả hai quả bóng đều màu đỏ.
Tổng số cách lấy 2 quả bóng từ 8 quả bóng là C(8, 2) = 8! / (2! * 6!) = 28.
Số cách lấy 2 quả bóng màu đỏ từ 5 quả bóng đỏ là C(5, 2) = 5! / (2! * 3!) = 10.
Vậy, xác suất để cả hai quả bóng đều màu đỏ là P(A) = 10 / 28 = 5 / 14.
b) Tính xác suất để có ít nhất một quả bóng màu xanh.
Có thể tính xác suất này bằng cách lấy 1 trừ đi xác suất để không có quả bóng màu xanh nào (tức là cả hai quả bóng đều màu đỏ).
P(B) = 1 - P(A) = 1 - 5/14 = 9/14.
c) Tính xác suất để hai quả bóng khác màu.
Số cách lấy 1 quả bóng đỏ và 1 quả bóng xanh là C(5, 1) * C(3, 1) = 5 * 3 = 15.
Vậy, xác suất để hai quả bóng khác màu là P(C) = 15 / 28.
Lưu ý khi giải bài tập 8.12 trang 63 SGK Toán 11 tập 2
- Đọc kỹ đề bài để xác định rõ yêu cầu của bài toán.
- Xác định đúng các công thức và quy tắc cần sử dụng.
- Tính toán cẩn thận để tránh sai sót.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Kết luận: Bài 8.12 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán về tổ hợp và xác suất. Việc nắm vững các công thức và quy tắc, cùng với việc luyện tập thường xuyên, sẽ giúp các em học sinh giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh đã hiểu rõ cách giải bài tập 8.12 trang 63 SGK Toán 11 tập 2. Chúc các em học tốt!