Bài 3.10 trang 74 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 3.10 trang 74 SGK Toán 11 tập 1 - Cùng khám phá
Bài 3.10 trang 74 SGK Toán 11 tập 1 thuộc chương 1: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
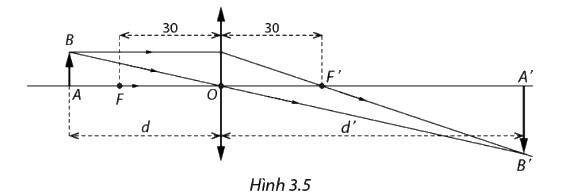
Một thấu kính hội tụ có tiêu cự f= 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang tâm của thấu kính một khoảng d (cm) > 30 (cm) thì được ảnh thật A’B’ của thấu kính một khoảng d’ (cm) ( Hình 3.5).
Đề bài
Một thấu kính hội tụ có tiêu cự f= 30 cm. Trong Vật lí, ta biết rằng nếu đặt vật thật AB cách quang tâm của thấu kính một khoảng d (cm) > 30 (cm) thì được ảnh thật A’B’ của thấu kính một khoảng d’ (cm) ( Hình 3.5). Ngược lại, nếu 0<d<30, ta có ảnh ảo. Công thức của thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{30}}\)
a, Từ công thức của thấu kính, hãy tìm biểu thức xác định hàm số d’= h (d)
b, Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {{30}^ + }} h(d),\mathop {\lim }\limits_{x \to {{30}^ - }} h(d)\) và \(\mathop {\lim }\limits_{x \to + \infty } h(d)\). Sử dụng các kết quả này để giải thích ý nghĩa đã biết trong Vật lí.
Phương pháp giải - Xem chi tiết
a, Từ công thức rút d’ theo d.
b, Sử dụng giới hạn trái, giới hạn phải, giới hạn tại vô cực.
Lời giải chi tiết
a, Ta có : \(h(d) = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{30}} \Rightarrow \frac{1}{{d'}} = \frac{1}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}} \Rightarrow d' = \frac{{30d}}{{d - 30}}\)
b, Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ + }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ + }} (d - 30) = 0\) và d-30 > 0
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ + }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to {{30}^ - }} 30d = 900\), \(\mathop {\lim }\limits_{d \to {{30}^ - }} (d - 30) = 0\) và d – 30 < 0
\( \Rightarrow \mathop {\lim }\limits_{d \to {{30}^ - }} h(d) = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \)
Ta có: \(\mathop {\lim }\limits_{d \to + \infty } h(d) = \mathop {\lim }\limits_{d \to + \infty } \frac{{30d}}{{d - 30}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{{30}}{d}}} = 30\).
Bài 3.10 trang 74 SGK Toán 11 tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 3.10 trang 74 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương Hàm số lượng giác. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức đã học về hàm số sin, cosin, tang, cotang để giải quyết các bài toán liên quan đến biên độ, chu kỳ, pha ban đầu và các tính chất khác của hàm số.
Nội dung bài tập:
Thông thường, bài 3.10 sẽ đưa ra một hàm số lượng giác cụ thể và yêu cầu học sinh thực hiện các thao tác sau:
- Xác định tập xác định của hàm số.
- Tìm chu kỳ của hàm số.
- Tìm biên độ của hàm số.
- Xác định pha ban đầu của hàm số.
- Vẽ đồ thị của hàm số.
- Giải các phương trình hoặc bất phương trình liên quan đến hàm số.
Lời giải chi tiết:
Để giải bài 3.10 trang 74 SGK Toán 11 tập 1 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Hàm số lượng giác cơ bản: Hiểu rõ định nghĩa, tập xác định, tập giá trị, tính tuần hoàn và các tính chất khác của các hàm số sin, cosin, tang, cotang.
- Biến đổi lượng giác: Thành thạo các công thức biến đổi lượng giác như công thức cộng, trừ, nhân đôi, chia đôi, hạ bậc, nâng bậc.
- Đồ thị hàm số lượng giác: Biết cách vẽ đồ thị của các hàm số lượng giác cơ bản và các hàm số lượng giác có dạng tổng quát.
Dưới đây là một ví dụ minh họa cách giải bài 3.10 (giả sử bài tập có dạng):
Bài tập: Tìm chu kỳ của hàm số y = 2sin(3x + π/4).
Lời giải:
Chu kỳ của hàm số y = sin(ax + b) là T = 2π/|a|. Trong trường hợp này, a = 3, vậy chu kỳ của hàm số y = 2sin(3x + π/4) là T = 2π/3.
Mẹo giải bài tập:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài tập và các thông tin đã cho.
- Sử dụng công thức: Áp dụng các công thức lượng giác phù hợp để biến đổi và giải bài tập.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
Tài liệu tham khảo:
Ngoài SGK Toán 11 tập 1, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán:
- Sách bài tập Toán 11 tập 1.
- Các trang web học Toán trực tuyến như tusach.vn, loigiaihay.com, vted.vn.
- Các video bài giảng Toán 11 trên YouTube.
Kết luận: Bài 3.10 trang 74 SGK Toán 11 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số lượng giác. Bằng cách nắm vững các kiến thức cơ bản, áp dụng các công thức phù hợp và luyện tập thường xuyên, các em sẽ có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
| Hàm số | Chu kỳ |
|---|---|
| y = sin(x) | 2π |
| y = cos(x) | 2π |
| y = tan(x) | π |
| Bảng chu kỳ của các hàm số lượng giác cơ bản | |