Giải mục 2 trang 17, 18 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 17, 18 SGK Toán 11 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 17, 18 SGK Toán 11 tập 1. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em hiểu rõ kiến thức và tự tin làm bài tập.
Bài viết này sẽ trình bày đầy đủ các bước giải, giải thích rõ ràng từng bước để các em có thể nắm bắt được phương pháp giải quyết các dạng bài tập tương tự.
Nếu cho b = a trong các công thức: (sin (a + b) = sin acos b + cos asin b;)
Hoạt động 2
Nếu cho b = a trong các công thức:
\(\sin (a + b) = \sin a\cos b + \cos a\sin b;\)
\(\cos (a + b) = \cos a\cos b - \sin a\sin b;\)
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\)
thì ta thu được các công thức nào?
Phương pháp giải:
Thay b = a vào các công thức trên.
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( {2a} \right) = \sin a\cos a + \cos a\sin a = 2\sin a\cos a;\\\cos \left( {2a} \right) = \cos a\cos a - \sin a\sin a = {\cos ^2}a - {\sin ^2}a;\\\tan \left( {2a} \right) = \frac{{\tan a + \tan a}}{{1 - \tan a\tan a}} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}.\end{array}\)
Luyện tập 2
a) Cho \(\cos \alpha = - \frac{1}{4}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\sin 2\alpha \) và \(\tan 2\alpha \).
b) Không dùng máy tính cầm tay, tính \(\cos 112,{5^0}\).
Phương pháp giải:
Áp dụng các hệ thức cơ bản của góc lượng giác, hệ thức giữa các góc lượng giác liên quan và công thức nhân đôi.
Lời giải chi tiết:
a) Ta có: \({\sin ^2}a = 1 - {\cos ^2}a = \frac{{15}}{{16}}\)
Mà \(\frac{\pi }{2} < \alpha < \pi \) nên \(\sin a = \frac{{\sqrt {15} }}{4}\)
\(\sin 2a = 2\sin a\cos a = \frac{{\sqrt {15} }}{4}.\left( { - \frac{1}{4}} \right) = - \frac{{\sqrt {15} }}{{16}}\)
\(\tan 2a = \frac{{\sin 2a}}{{\cos 2a}} = \frac{{\sqrt {15} }}{4}:\left( { - \frac{1}{4}} \right) = - \sqrt {15} \)
b) Ta có: \(\cos {225^0} = \cos \left( {{{45}^0} + {{180}^0}} \right) = - \cos {45^0} = - \frac{{\sqrt 2 }}{2}\)
\({\cos ^2}112,{5^0} = \frac{{1 + \cos {{225}^0}}}{2} = \frac{{1 - \frac{{\sqrt 2 }}{2}}}{2} = \frac{{2 - \sqrt 2 }}{4}\)
\( \Rightarrow \cos 112,{5^0} = - \sqrt {\frac{{2 - \sqrt 2 }}{4}} = - \frac{{\sqrt {2 - \sqrt 2 } }}{2}\)
Vận dụng 2
Một quả bóng golf kể từ lúc được đánh đến lúc chạm mặt đất đã di chuyển được một khoảng cách d (m) theo phương nằm ngang. Biết rằng \(d = \frac{{v_0^2\sin 2\theta }}{g}\), trong đó \({v_0}\) (m/s) là vận tốc ban đầu của quả bóng, g là gia tốc trọng trường và \(\theta \) là góc đánh quả bóng so với phương nằm ngang (nguồn: https://pressbooks.uiowa.edu/clonedbook/chapter/projectile-motion/). Tính giá trị của \(\cos 2\theta \) và \(\sin \theta \) khi \({v_0}\)= 15 m/s, d = 12,5 m, g = 10 m/s2 và \({0^0} < \theta < {45^0}\).
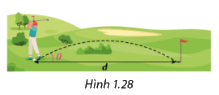
Phương pháp giải:
Áp dụng hệ thức cơ bản giữa các góc lượng giác và công thức nhân đôi.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}d = \frac{{v_0^2\sin 2\theta }}{g}\\ \Leftrightarrow 12,5 = \frac{{{{15}^2}.\sin 2\theta }}{{10}}\\ \Rightarrow \sin 2\theta = \frac{5}{9}\end{array}\)
Lại có: \({\cos ^2}2\theta = 1 - {\sin ^2}2\theta = \frac{{56}}{{81}}\)
Mà \({0^0} < \theta < {45^0} \Rightarrow {0^0} < 2\theta < {90^0}\)\( \Rightarrow \cos 2\theta = \frac{{2\sqrt {14} }}{9}\)
\({\sin ^2}\theta = \frac{{1 - \cos 2\theta }}{2} = \frac{{9 - 2\sqrt {14} }}{{18}}\)
Mà \({0^0} < \theta < {45^0}\)\( \Rightarrow \sin \theta = \sqrt {\frac{{9 - 2\sqrt {14} }}{{18}}} \)
Giải mục 2 trang 17, 18 SGK Toán 11 tập 1 - Cùng khám phá: Tổng quan và Phương pháp
Mục 2 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 11.
Nội dung chính của Mục 2
- Phép tịnh tiến: Định nghĩa, tính chất, và ứng dụng của phép tịnh tiến trong hình học.
- Phép quay: Định nghĩa, tính chất, và ứng dụng của phép quay trong hình học.
- Phép đối xứng trục: Định nghĩa, tính chất, và ứng dụng của phép đối xứng trục trong hình học.
- Phép đối xứng tâm: Định nghĩa, tính chất, và ứng dụng của phép đối xứng tâm trong hình học.
- Bài tập vận dụng: Các bài tập giúp học sinh rèn luyện kỹ năng và hiểu sâu hơn về các phép biến hình.
Giải chi tiết các bài tập trang 17, 18
Bài 1: (Trang 17)
Bài 1 thường yêu cầu học sinh xác định ảnh của một điểm hoặc một hình qua một phép biến hình cho trước. Để giải bài này, các em cần nắm vững định nghĩa và tính chất của phép biến hình đó. Ví dụ, nếu đề bài yêu cầu tìm ảnh của điểm A(x0, y0) qua phép tịnh tiến theo vectơ v = (a, b), thì ảnh A' của A sẽ có tọa độ A'(x0 + a, y0 + b).
Bài 2: (Trang 18)
Bài 2 có thể yêu cầu học sinh chứng minh một tính chất liên quan đến các phép biến hình. Để giải bài này, các em cần sử dụng các định lý và tính chất đã học trong sách giáo khoa. Ví dụ, để chứng minh hai đường thẳng song song, các em có thể sử dụng tính chất của phép tịnh tiến hoặc phép quay.
Bài 3: (Trang 18)
Bài 3 thường là một bài tập ứng dụng thực tế, yêu cầu học sinh sử dụng các kiến thức về phép biến hình để giải quyết một vấn đề cụ thể. Để giải bài này, các em cần phân tích đề bài một cách cẩn thận và tìm ra mối liên hệ giữa các yếu tố trong bài toán với các phép biến hình đã học.
Mẹo học tốt Toán 11 - Chương Phép biến hình
- Nắm vững định nghĩa và tính chất: Đây là nền tảng cơ bản để giải quyết mọi bài tập liên quan đến phép biến hình.
- Vẽ hình: Vẽ hình giúp các em hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau giúp các em rèn luyện kỹ năng và hiểu sâu hơn về các phép biến hình.
- Sử dụng tài liệu tham khảo: Sách bài tập, đề thi thử, và các trang web học tập trực tuyến có thể cung cấp thêm nhiều bài tập và lời giải hữu ích.
Bảng tóm tắt các phép biến hình
| Phép biến hình | Định nghĩa | Tính chất |
|---|---|---|
| Phép tịnh tiến | Biến mỗi điểm thành một điểm sao cho vectơ nối hai điểm bằng vectơ tịnh tiến. | Bảo toàn khoảng cách, bảo toàn góc. |
| Phép quay | Biến mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc tạo bởi hai đoạn thẳng nối tâm quay với điểm cũ và điểm mới là góc quay. | Bảo toàn khoảng cách, bảo toàn góc. |
| Phép đối xứng trục | Biến mỗi điểm thành một điểm sao cho trục đối xứng là đường trung trực của đoạn thẳng nối hai điểm. | Bảo toàn khoảng cách, biến đường thẳng thành đường thẳng song song hoặc trùng nhau. |
| Phép đối xứng tâm | Biến mỗi điểm thành một điểm sao cho tâm đối xứng là trung điểm của đoạn thẳng nối hai điểm. | Bảo toàn khoảng cách, biến đường thẳng thành đường thẳng song song hoặc trùng nhau. |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn khi giải bài tập mục 2 trang 17, 18 SGK Toán 11 tập 1. Chúc các em học tập tốt!