Giải mục 2 trang 17, 18, 19 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 17, 18, 19 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 17, 18, 19 SGK Toán 11 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 2 này tập trung vào các kiến thức quan trọng về... (điền kiến thức trọng tâm của mục 2). Việc nắm vững kiến thức này là nền tảng cho các bài học tiếp theo.
Một thí nghiệm cho thấy trong điều kiện môi trường sống lí tưởng
Câu 1
Một thí nghiệm cho thấy trong điều kiện môi trường sống lí tưởng và thức ăn dồi dào thì số lượng của một đàn chuột sẽ gấp đôi sau 55 ngày (nguồn: https://baotintuc.vn/ho-so/ky-la-thi-nghiem-xay-dung-xa-hoi-khong-tuong-cho-chuot-20181226104302132.htm).
Giả sử lúc đầu, đàn chuột có 100 con. Như vậy, sau thời gian t ngày, số lượng chuột là \(P = {100.2^{\frac{t}{{55}}}}\) con.
a) Mất bao lâu để đàn chuột đạt số lượng 2 000 con?
b) Tìm một hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P (nếu có).
Phương pháp giải:
Thay P = 2000 vào \(P = {100.2^{\frac{t}{{55}}}}\). Tìm t.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}{100.2^{\frac{t}{{55}}}} = 2000\\ \Leftrightarrow {2^{\frac{t}{{55}}}} = 20\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}20\\ \Leftrightarrow t = 55.{\log _2}20\\ \Leftrightarrow t \approx 237,71\end{array}\)
b)
\(\begin{array}{l}P = {100.2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{P}{{100}} = {2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}\frac{P}{{100}}\\ \Leftrightarrow t = 55.{\log _2}\frac{P}{{100}}\end{array}\)
Vậy hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P là: \(t = 55.{\log _2}\frac{P}{{100}}\)
Luyện tập 3
Tìm tập xác định của hàm số sau:
a) \(y = \log \left( {2x - 3} \right)\)
b) \(y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)\)
c) \(y = \ln \frac{{3x + 2}}{{1 - x}}\)
Phương pháp giải:
Hàm số \(y = {\log _a}\left( {u\left( x \right)} \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).
Lời giải chi tiết:
a) \(y = \log \left( {2x - 3} \right)\) xác định khi \(2x - 3 > 0 \Leftrightarrow x > \frac{3}{2}\)
Vậy \(D = \left( {\frac{3}{2}; + \infty } \right)\)
b) \(y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)\) xác định khi \({x^2} - 1 > 0 \Leftrightarrow {x^2} > 1 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\)
Vậy \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)
c) \(y = \ln \frac{{3x + 2}}{{1 - x}}\) xác định khi \(\frac{{3x + 2}}{{1 - x}} > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3x + 2 > 0\\1 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}3x + 2 < 0\\1 - x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > - \frac{2}{3}\\x < 1\end{array} \right.\\\left\{ \begin{array}{l}x < - \frac{2}{3}\\x > 1\end{array} \right.\,{\rm{(L)}}\end{array} \right.\)
Vậy \(D = \left( {\frac{{ - 2}}{3};1} \right)\)
Hoạt động 4
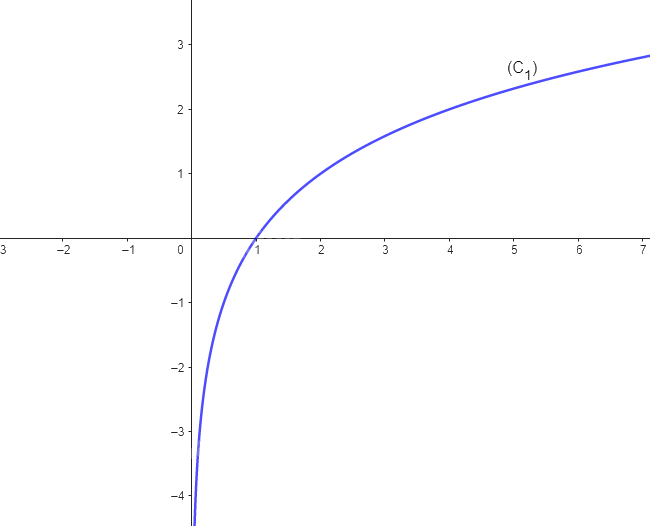
Cho hàm số \(y = {\log _2}x\) có đồ thị là (C1) và hàm số \(y = {\log _{0,5}}x\) có đồ thị (C2).
a) Hoàn thành bảng giá trị sau và biểu diễn trên hệ trục Oxy.
b) Vẽ đường cong nối các điểm thuộc (C1) (theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C2) (theo thứ tự hoành độ tăng dần).
Phương pháp giải:
Thay lần lượt các giá trị của x vào hàm số.
Lời giải chi tiết:
a,

b,
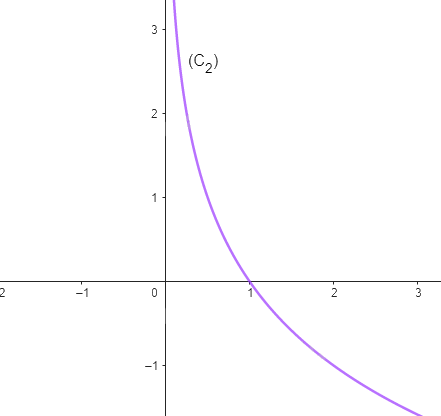
Luyện tập 4
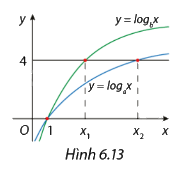
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như Hình 6.13. Đường thẳng y = 4 cắt hai đồ thị tại các điểm có hoành độ x1, x2. Biết rằng x1 = 2x2. Tính giá trị của \(\frac{a}{b}\).

Phương pháp giải:
Thay y = 4 vào 2 hàm số. Áp dụng: \({\log _a}b = c \Leftrightarrow {a^c} = b\) để tính a, b lần lượt theo \({x_1},{x_2}\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\log _a}{x_1} = 4\\ \Leftrightarrow {a^4} = {x_1}\\ \Leftrightarrow {a^4} = 2{x_2}\\ \Leftrightarrow a = {\left( {2{x_2}} \right)^{\frac{1}{4}}}\end{array}\)
\(\begin{array}{l}{\log _b}{x_2} = 4\\ \Leftrightarrow {b^4} = {x_2}\\ \Leftrightarrow b = {\left( {{x_2}} \right)^{\frac{1}{4}}}\end{array}\)
\( \Rightarrow \frac{a}{b} = \frac{{{{\left( {2{x_2}} \right)}^{\frac{1}{4}}}}}{{{{\left( {{x_2}} \right)}^{\frac{1}{4}}}}} = {2^{\frac{1}{4}}}\)
Giải mục 2 trang 17, 18, 19 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 11 tập 2 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc hiểu rõ các tính chất và ứng dụng của các phép biến hình này là vô cùng quan trọng để giải quyết các bài toán hình học một cách hiệu quả.
Nội dung chính của Mục 2
- Phép tịnh tiến: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép tịnh tiến.
- Phép quay: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép quay.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng trục.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách xác định ảnh của một điểm, một đường thẳng, một đường tròn qua phép đối xứng tâm.
- Kết hợp các phép biến hình: Cách thực hiện và tính chất của việc kết hợp các phép biến hình.
Hướng dẫn giải các bài tập trong Mục 2
Để giải các bài tập trong Mục 2, các em cần nắm vững các kiến thức sau:
- Xác định phép biến hình: Đọc kỹ đề bài để xác định phép biến hình được sử dụng trong bài toán.
- Áp dụng định nghĩa và tính chất: Sử dụng định nghĩa và tính chất của phép biến hình để tìm ra mối quan hệ giữa các đối tượng hình học.
- Sử dụng công thức: Áp dụng các công thức liên quan đến phép biến hình để tính toán các thông số cần thiết.
- Vẽ hình: Vẽ hình minh họa để giúp các em hình dung rõ hơn về bài toán và tìm ra lời giải.
Giải chi tiết các bài tập trang 17, 18, 19
Dưới đây là giải chi tiết các bài tập trang 17, 18, 19 SGK Toán 11 tập 2:
Bài 1: (Trang 17)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 2: (Trang 18)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, kèm theo hình vẽ minh họa nếu cần thiết)
Bài 3: (Trang 19)
(Nêu lại đề bài)
Lời giải:
(Giải chi tiết bài tập, kèm theo hình vẽ minh họa nếu cần thiết)
Lưu ý quan trọng
Khi giải các bài tập về phép biến hình, các em cần chú ý đến thứ tự thực hiện các phép biến hình. Nếu có nhiều phép biến hình được thực hiện liên tiếp, các em cần thực hiện chúng theo đúng thứ tự từ trái sang phải.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trong Mục 2 trang 17, 18, 19 SGK Toán 11 tập 2, các em sẽ hiểu rõ hơn về các kiến thức về phép biến hình và tự tin giải quyết các bài toán liên quan. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!