Giải mục 1 trang 21, 22 SGK Toán 11 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 21, 22 SGK Toán 11 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.

Với mục tiêu hỗ trợ tối đa cho quá trình học tập của các em, tusach.vn đã biên soạn bộ giải bài tập Toán 11 tập 2 đầy đủ và chính xác.

Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {a^x}\) và đường thẳng y = b.

Hoạt động 1

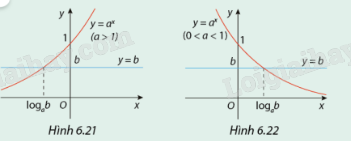
Giải mục 1 trang 21, 22 SGK Toán 11 tập 2 - Cùng khám phá 1

Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {a^x}\) và đường thẳng y = b.

Phương pháp giải:

Quan sát hình vẽ.

Lời giải chi tiết:

Ta có phương trình hoành độ giao điểm \({a^x} = b\)

Nếu b > 0 thì phương trình có nghiệm duy nhất là \(x = {\log _a}b\)

Nếu \(b \le 0\)thì phương trình vô nghiệm.

Luyện tập 1

Giải các phương trình:

a) \({2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\)

b) \(1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\)

Phương pháp giải:

Với \(a > 0,a \ne 1\), ta có: \({a^{A\left( x \right)}} = {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) = B\left( x \right)\,\)

Lời giải chi tiết:

\(\begin{array}{l}{2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\\ \Leftrightarrow {2.3^2}{.3^{x - 1}} - {6.3^{x - 1}} - {3.3^{x - 1}} = 9\\ \Leftrightarrow {3^{x - 1}}\left( {{{2.3}^2} - 6 - 3} \right) = 9\\ \Leftrightarrow {3^{x - 1}}.9 = 9\\ \Leftrightarrow {3^{x - 1}} = 1\\ \Leftrightarrow {3^{x - 1}} = {3^0}\\ \Leftrightarrow x - 1 = 0\\ \Leftrightarrow x = 1\end{array}\)

Vậy phương trình có nghiệm là x = 1.

\(\begin{array}{l}1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{1}{{\frac{2}{3}}}} \right)^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow \frac{1}{{{{\left( {\frac{2}{3}} \right)}^{5x - 7}}}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{x + 1}}.{\left( {\frac{2}{3}} \right)^{5x - 7}} = 1\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{6x - 6}} = {\left( {\frac{2}{3}} \right)^0}\\ \Leftrightarrow 6x - 6 = 0\\ \Leftrightarrow x = 1\end{array}\)

Vậy phương trình có nghiệm x = 1.

Giải mục 1 trang 21, 22 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải

Mục 1 trang 21, 22 SGK Toán 11 tập 2 tập trung vào việc ôn tập chương trình Đại số và Giải tích, đặc biệt là các kiến thức về hàm số, đồ thị hàm số, và các phép biến đổi hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.

Nội dung chính của Mục 1

Ôn tập về hàm số: Khái niệm hàm số, tập xác định, tập giá trị, tính đơn điệu, cực trị của hàm số.
Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị hàm số.
Các phép biến đổi hàm số: Biến đổi đồ thị hàm số bằng các phép tịnh tiến, phép co giãn, phép đối xứng.

Hướng dẫn giải chi tiết các bài tập trong Mục 1

Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 1 trang 21, 22 SGK Toán 11 tập 2:

Bài 1: (Trang 21)

Bài 1 yêu cầu xác định tập xác định của hàm số. Để giải bài này, các em cần nắm vững điều kiện xác định của các hàm số cơ bản như hàm phân thức, hàm căn bậc hai, hàm logarit.

Ví dụ: Hàm số y = √(x-2) có tập xác định là x ≥ 2.

Bài 2: (Trang 21)

Bài 2 yêu cầu xét tính chẵn lẻ của hàm số. Để giải bài này, các em cần hiểu rõ định nghĩa về hàm số chẵn, hàm số lẻ và cách kiểm tra tính chẵn lẻ của hàm số.

Ví dụ: Hàm số y = x² là hàm số chẵn vì y(-x) = y(x).

Bài 3: (Trang 22)

Bài 3 yêu cầu vẽ đồ thị hàm số. Để giải bài này, các em cần xác định các điểm đặc biệt của đồ thị hàm số như giao điểm với các trục tọa độ, điểm cực trị, điểm uốn. Sau đó, các em có thể vẽ đồ thị hàm số bằng cách nối các điểm này lại với nhau.

Mẹo giải nhanh và hiệu quả

Nắm vững định nghĩa và tính chất: Đây là nền tảng quan trọng để giải quyết mọi bài toán.
Sử dụng các công cụ hỗ trợ: Các em có thể sử dụng máy tính cầm tay hoặc các phần mềm vẽ đồ thị để kiểm tra lại kết quả của mình.
Luyện tập thường xuyên: Càng luyện tập nhiều, các em càng trở nên thành thạo và tự tin hơn.

Tài liệu tham khảo hữu ích

Ngoài SGK Toán 11 tập 2, các em có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11 tập 2
Các trang web học Toán trực tuyến
Các video bài giảng Toán 11 trên YouTube

Hy vọng với những hướng dẫn chi tiết này, các em sẽ giải quyết thành công các bài tập trong Mục 1 trang 21, 22 SGK Toán 11 tập 2. Chúc các em học tập tốt!

Bài tập	Nội dung	Mức độ khó
Bài 1	Xác định tập xác định	Dễ
Bài 2	Xét tính chẵn lẻ	Trung bình
Bài 3	Vẽ đồ thị hàm số	Khó

Giải mục 1 trang 21, 22 SGK Toán 11 tập 2 - Cùng khám phá