Bài 8.20 trang 72 SGK Toán 11 tập 2

Bài 8.20 trang 72 SGK Toán 11 tập 2 - Cùng khám phá

Bài 8.20 thuộc chương trình Toán 11 tập 2, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các công thức lượng giác để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.

Kim tự tháp Cheops của Ai Cập (còn gọi là kim tự tháp Khufu, được xây dựng vào khoảng 2 500 năm trước Công nguyên)

Đề bài

Kim tự tháp Cheops của Ai Cập (còn gọi là kim tự tháp Khufu, được xây dựng vào khoảng 2 500 năm trước Công nguyên) có dạng là một hình chóp tử giác đều với cạnh đáy dài khoảng 230 m và chiều cao khoảng 147m (Hình 8.48).

Bài 8.20 trang 72 SGK Toán 11 tập 2 - Cùng khám phá 1

a) Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp này.

b) Tính số đo của các góc nhị diện tạo bởi mặt bên và mặt đáy của kim tự tháp. (Nguồn : https://www.congluan.vn/dai-kim-tu-thap-giza-van-ky-la-va-bi-an-voi-cac-nha-khoa-hoc-post203156.html)

Phương pháp giải - Xem chi tiết Bài 8.20 trang 72 SGK Toán 11 tập 2 - Cùng khám phá 2

Chóp tứ giác đều có đáy là hình vuông và đường cao đi qua tâm đáy.

a) Áp dụng Py-ta-go.

Diện tích xung quanh bằng 4 lần diện tích tam giác SBC.

b) - Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):

+ Tìm giao tuyến d của (SCD) và (ACD).

+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.

+ Tính \(\left( {a,b} \right)\).

- Áp dụng định lý Cosin.

Lời giải chi tiết

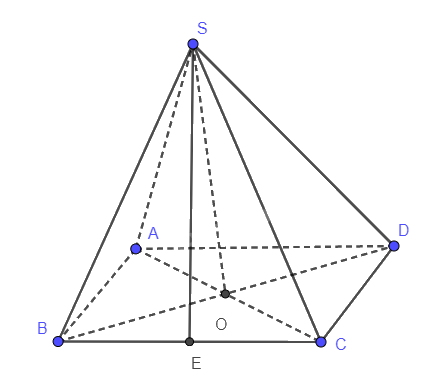
Bài 8.20 trang 72 SGK Toán 11 tập 2 - Cùng khám phá 3

a) Ta có: \(BD = \sqrt {B{C^2} + C{D^2}} = \sqrt {{{230}^2} + {{230}^2}} = 230\sqrt 2 \)

\( \Rightarrow BO = 115\sqrt 2 \)

\( \Rightarrow SB = \sqrt {S{O^2} + B{O^2}} = \sqrt {{{147}^2} + {{\left( {115\sqrt 2 } \right)}^2}} \approx 219\) (m)

Gọi E là trung điểm của BC. Tam giác SBC cân tại S nên SE vuông góc với BC

\(BE = \frac{{230}}{2} = 115\)

\(SE = \sqrt {S{B^2} - B{E^2}} = \sqrt {{{219}^2} - {{115}^2}} \approx 186\)

\({S_{\Delta SBC}} = \frac{1}{2}.186.230 = 21390\)

Diện tích xung quanh là: \(21390.4 = 85560\)

b) Ta có:

SA vuông góc với AB

AD vuông góc với AB

Nên góc phẳng nhị diện tạo bởi (SAB) và (ABCD) là góc SAD

\(\cos \widehat {SAD} = \frac{{S{A^2} + A{D^2} - S{D^2}}}{{2SA.AD}} = \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}}\)

\( \Rightarrow \widehat {SAD} \approx {58^0}\)

Bài 8.20 trang 72 SGK Toán 11 tập 2: Giải chi tiết và hướng dẫn

Bài 8.20 trang 72 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình ôn tập chương 3 về hàm số lượng giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Hàm số lượng giác cơ bản: sin, cos, tan, cot và các tính chất của chúng.
Đường tròn lượng giác: Hiểu rõ mối liên hệ giữa các giá trị lượng giác và vị trí trên đường tròn lượng giác.
Các công thức lượng giác: Công thức cộng, trừ, nhân đôi, chia đôi, hạ bậc, nâng bậc.
Phương pháp giải phương trình lượng giác: Sử dụng các phép biến đổi lượng giác để đưa phương trình về dạng cơ bản.

Nội dung bài tập:

Bài 8.20 thường yêu cầu học sinh giải các phương trình lượng giác, chứng minh các đẳng thức lượng giác hoặc tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác. Dưới đây là một ví dụ minh họa:

Ví dụ minh họa:

Giải phương trình: 2sin²x - 3sinx + 1 = 0

Đặt t = sinx: Phương trình trở thành 2t² - 3t + 1 = 0
Giải phương trình bậc hai: Δ = (-3)² - 4 * 2 * 1 = 1. Suy ra t₁ = 1, t₂ = 1/2
Tìm x:

Nếu sinx = 1 thì x = π/2 + kπ, k ∈ Z
Nếu sinx = 1/2 thì x = π/6 + k2π hoặc x = 5π/6 + k2π, k ∈ Z

Lời khuyên khi giải bài tập:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Sử dụng các công thức lượng giác một cách chính xác.
Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Luyện tập thường xuyên để nâng cao kỹ năng giải toán.

Tusach.vn luôn đồng hành cùng học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh tự tin giải quyết các bài tập Toán 11. Ngoài ra, chúng tôi còn có nhiều tài liệu học tập hữu ích khác, như bài giảng, bài tập trắc nghiệm, và các video hướng dẫn.

Các bài tập tương tự:

Bài 8.19 trang 72 SGK Toán 11 tập 2
Bài 8.21 trang 72 SGK Toán 11 tập 2

Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 8.20 trang 72 SGK Toán 11 tập 2 và tự tin hơn trong quá trình học tập. Chúc các em học tốt!

Bài 8.20 trang 72 SGK Toán 11 tập 2 - Cùng khám phá

Bài 8.20 trang 72 SGK Toán 11 tập 2

Bài 8.20 trang 72 SGK Toán 11 tập 2: Giải chi tiết và hướng dẫn

Ví dụ minh họa:

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN