Giải mục 1 trang 33, 34, 35 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 33, 34, 35 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 33, 34, 35 SGK Toán 11 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng linh hoạt vào các bài tập khác.
Một vật bắt đầu chuyển động theo đường thẳng và quãng đường đi được sau t giây được tính bởi (s(t) = 2{t^2}), s(t) tính bằng mét.
Hoạt động 1
Một vật bắt đầu chuyển động theo đường thẳng và quãng đường đi được sau t giây được tính bởi \(s(t) = 2{t^2}\), s(t) tính bằng mét.
a, Cho biết vận tốc trung bình ( đơn vị m/s) của vật trong khoảng thời gian [\({t_0};t\)] được tính bởi công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\). Hãy tính vận tốc trung bình trong các khoảng thời gian [\({t_0};t\)] với \({t_0} = 3\)và t lần lượt là 3,1 ; 3,01 ; 3,001. Sau đó hoàn thành Bảng 7.1
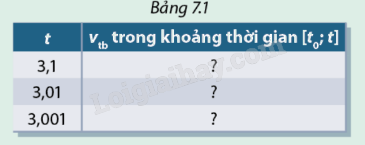
b, Vận tốc trung bình trong khoảng thời gian nào ở Bảng 7.1 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình trong khoảng thời gian [\({t_0};t\)] càng gần với vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t như thế nào?
Phương pháp giải:
a, Áp dụng công thức \(s(t) = 2{t^2}\) và công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\) để tính vận tốc trung bình.
b, Dựa vào kết quả câu a để tìm giá trị vận tốc gần với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).
Lời giải chi tiết:
a, Thay t = 3,1; t=3,01; t= 3,001 vào hàm số s(t) ta được:
\(s(3,1) = 2.3,{1^2} = 2.9,61 = 19,22\)\( \Rightarrow {v_{tb}} = \frac{{s(3,1) - s(3)}}{{3,1 - 3}} = \frac{{19,22 - 18}}{{0,1}} = 12,2\)
\(s(3,01) = 2.3,{01^2} = 2.9,0601 = 18,1202\)\( \Rightarrow {v_{tb}} = \frac{{s(3,01) - s(3)}}{{3,01 - 3}} = \frac{{18,1202 - 18}}{{0,01}} = 12,02\)
\(s(3,001) = 2.3,{001^2} = 2.9,006001 = 18,012002\)\( \Rightarrow {v_{tb}} = \frac{{s(3,001) - s(3)}}{{3,001 - 3}} = \frac{{18,012002 - 18}}{{0,001}} = 12,002\)

b, Từ kết quả câu a cho thấy vận tốc tại thời điểm t = 3,001 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Từ kết quả câu b ta thấy để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).
Luyện tập 1
Tính đạo hàm của hàm số \(f(x) = \frac{2}{{x + 1}}\) tại điểm \({x_0} = 1\)
Phương pháp giải:
Sử dụng định nghĩa đạo hàm của hàm số tại một điểm
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{2}{{x + 1}} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{(x + 1).(x - 1)}}\mathop { = \lim }\limits_{x \to 1} \frac{{ - 1}}{{x + 1}} = \frac{{ - 1}}{2}\)
Vận dụng
Xét tình huống vận động viên nhảy dù trong bài toán khởi động:
a, Tìm vận tốc của vận động viên nhảy dù sau 2 giây kể từ khi bắt đầu rơi tự do
b, Sau khi rơi tự do được 490 m, vận động viên đó bung dù để chuẩn bị đáp xuống mặt đất. Tìm vận tốc của vận động viên tại thời điểm bung dù.
Phương pháp giải:
a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là đạo hàm của hàm số tại \({t_0} = 2\).
b, Tìm thời điểm mà vận động viên đi được 490 m, sau đó tính đạo hàm của hàm số tại thời điểm đó để xác định vận tốc tức thời.
Lời giải chi tiết:
a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là:
\(\mathop {\lim }\limits_{t \to 2} \frac{{f(t) - f(2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 19,6}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 4)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 2).(t + 2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} 4,9.(t + 2) = 19,6\)
Vậy vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là 19,6 m / s
b, Ta có: \(s({t_1}) = 4,9{t_1}^2 \Leftrightarrow 490 = 4,9.{t_1}^2 \Leftrightarrow {t_1}^2 = 100 \Rightarrow {t_1} = 10\)
Vận tốc của vận động viên tại thời điểm bung dù là:
\(\mathop {\lim }\limits_{t \to 10} \frac{{f(t) - f(10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 490}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 100)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 10).(t + 10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 10} 4,9.(t + 10) = 98\)
Vậy vận tốc của vận động viên tại thời điểm bung dù là 98 m/s
Giải mục 1 trang 33, 34, 35 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 1 của SGK Toán 11 tập 2 thường xoay quanh các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các tính chất và ứng dụng của các phép biến hình này là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong SGK mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Nội dung chi tiết Giải mục 1 trang 33, 34, 35
Để giúp các em hiểu rõ hơn về nội dung này, tusach.vn sẽ trình bày chi tiết lời giải của từng bài tập trong mục 1 trang 33, 34, 35 SGK Toán 11 tập 2.
Bài 1: (Trang 33)
Bài 1 thường yêu cầu các em xác định ảnh của một điểm hoặc một hình qua một phép biến hình cho trước. Để giải bài này, các em cần nắm vững định nghĩa và tính chất của phép biến hình đó. Ví dụ, nếu đề bài yêu cầu tìm ảnh của điểm A(x0, y0) qua phép tịnh tiến theo vectơ v = (a, b), thì ảnh của A sẽ là A'(x0 + a, y0 + b).
Bài 2: (Trang 34)
Bài 2 có thể yêu cầu các em chứng minh một tính chất liên quan đến phép biến hình. Để giải bài này, các em cần sử dụng các định lý và tính chất đã học trong sách giáo khoa. Ví dụ, để chứng minh hai đường thẳng song song khi ảnh của chúng qua một phép biến hình cũng song song, các em cần sử dụng tính chất bảo toàn tính song song của phép biến hình đó.
Bài 3: (Trang 35)
Bài 3 thường là một bài tập ứng dụng, yêu cầu các em sử dụng kiến thức về phép biến hình để giải quyết một bài toán thực tế. Để giải bài này, các em cần phân tích bài toán, xác định các yếu tố liên quan đến phép biến hình và áp dụng các công thức và tính chất đã học.
Phương pháp giải các bài tập về phép biến hình
- Xác định phép biến hình: Đọc kỹ đề bài để xác định phép biến hình được sử dụng trong bài toán.
- Nắm vững định nghĩa và tính chất: Ôn lại định nghĩa và tính chất của phép biến hình đó.
- Áp dụng công thức: Sử dụng các công thức và tính chất đã học để giải bài toán.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa
Ví dụ: Cho điểm A(1, 2) và vectơ t = (3, -1). Tìm ảnh A' của điểm A qua phép tịnh tiến theo vectơ t.
Giải:
A' = A + t = (1 + 3, 2 - 1) = (4, 1)
Lưu ý khi giải bài tập
- Luôn vẽ hình để minh họa cho bài toán.
- Sử dụng các ký hiệu toán học một cách chính xác.
- Kiểm tra lại kết quả trước khi nộp bài.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ tự tin hơn trong việc học tập môn Toán 11. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Phép biến hình | Công thức biến đổi |
|---|---|
| Phép tịnh tiến | M'(x' , y') = M(x + a, y + b) |
| Phép quay | M'(x' , y') = M(xcosα - ysinα, xsinα + ycosα) |