Giải mục 1 trang 8, 9 SGK Toán 11 tập 2 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 8, 9 SGK Toán 11 tập 2. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.

tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.

Tìm một số thích hợp cho mỗi dấu "?" trong bảng sau, biết \(b = {2^\alpha }\):

Hoạt động 1

Tìm một số thích hợp cho mỗi dấu "?" trong bảng sau, biết \(b = {2^\alpha }\):

Giải mục 1 trang 8, 9 SGK Toán 11 tập 2 - Cùng khám phá 1

Phương pháp giải:

Thay \(\alpha \) = -2, -3 vào \(b = {2^\alpha }\) để tìm b tương ứng.

Thay b = 16, \(\sqrt 2 \), \(\frac{1}{4}\) vào \(b = {2^\alpha }\) để tìm \(\alpha \) tương ứng.

Lời giải chi tiết:

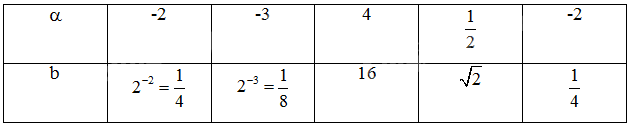
Giải mục 1 trang 8, 9 SGK Toán 11 tập 2 - Cùng khám phá 2

Hoạt động 2

Từ Định nghĩa, với a > 0, \(a \ne 1\) và b > 0, ta có:

\(\alpha = {\log _a}b\,\left( 1 \right) \Leftrightarrow {a^\alpha } = b\left( 2 \right).\)

Tìm một số hoặc biểu thức thích hợp cho mỗi ô ?:

a) Từ (1), khi b = 1 thì \(\alpha \) = ?;

b) Từ (1), khi b = a thì \(\alpha \) = ?;

c) Thay b từ (2) vào (1), ta được ?;

d) Thay \(\alpha \) từ (1) vào (2), ta được ?.

Phương pháp giải:

a) \({\log _a}1 = 0\)

b) \({\log _a}a = 1\)

c) \({\log _a}\left( {{a^\alpha }} \right) = \alpha \)

d) \({a^{{{\log }_a}b}} = b\)

Lời giải chi tiết:

a) \({\log _a}1 = 0 \Rightarrow \alpha = 0\)

b) \({\log _a}a = 1 \Rightarrow \alpha = 1\)

c) \({\log _a}\left( {{a^\alpha }} \right) = \alpha \)

d) \({a^{{{\log }_a}b}} = b\)

Luyện tập 1

Tính \(\log 1000;{\log _{\frac{1}{{\sqrt 3 }}}}9;{\log _2}{4^{\frac{1}{7}}}\) và \({\left( {\frac{1}{{25}}} \right)^{{{\log }_5}\frac{1}{3}}}\).

Phương pháp giải:

Áp dụng: \({\log _a}\left( {{a^\alpha }} \right) = \alpha \) và \({a^{{{\log }_a}b}} = b\)

Lời giải chi tiết:

\(\log 1000 = \log \left( {{{10}^3}} \right) = 3\)

\({\log _{\frac{1}{{\sqrt 3 }}}}9 = {\log _{\frac{1}{{\sqrt 3 }}}}\left( {{{\left( {\frac{1}{{\sqrt 3 }}} \right)}^{ - 4}}} \right) = - 4\)

\({\log _2}{4^{\frac{1}{7}}} = {\log _2}\left( {{2^{\frac{2}{7}}}} \right) = \frac{2}{7}\)

Giải mục 1 trang 8, 9 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải

Mục 1 trang 8, 9 SGK Toán 11 tập 2 thường xoay quanh các kiến thức cơ bản về đạo hàm, bao gồm định nghĩa, ý nghĩa hình học và các quy tắc tính đạo hàm của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.

Nội dung chính của Mục 1 trang 8, 9

Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
Ý nghĩa hình học của đạo hàm: Nhận biết mối liên hệ giữa đạo hàm và hệ số góc của tiếp tuyến của đồ thị hàm số.
Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
Đạo hàm của một số hàm số cơ bản: Biết cách tính đạo hàm của các hàm số thường gặp như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.

Phương pháp giải bài tập Mục 1 trang 8, 9

Xác định đúng công thức đạo hàm cần sử dụng: Dựa vào dạng hàm số và yêu cầu của bài toán để chọn công thức đạo hàm phù hợp.
Thực hiện các phép biến đổi đại số: Đơn giản hóa biểu thức trước khi tính đạo hàm để tránh sai sót.
Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả bằng cách thay các giá trị cụ thể vào để đảm bảo tính chính xác.

Giải chi tiết các bài tập trong Mục 1 trang 8, 9

Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 8, 9 SGK Toán 11 tập 2:

Bài 1: Tính đạo hàm của các hàm số sau

a) f(x) = x³ - 2x² + 5x - 1

Lời giải: f'(x) = 3x² - 4x + 5

b) g(x) = sin(x) + cos(x)

Lời giải: g'(x) = cos(x) - sin(x)

Bài 2: Tìm đạo hàm của hàm số y = (x² + 1) / (x - 1)

Lời giải: Sử dụng quy tắc đạo hàm của thương:

y' = [(x² + 1)'(x - 1) - (x² + 1)(x - 1)'] / (x - 1)²

y' = [2x(x - 1) - (x² + 1)] / (x - 1)²

y' = (x² - 2x - 1) / (x - 1)²

Bài 3: Tính đạo hàm của hàm số y = e^x * sin(x)

Lời giải: Sử dụng quy tắc đạo hàm của tích:

y' = (e^x)' * sin(x) + e^x * (sin(x))'

y' = e^x * sin(x) + e^x * cos(x)

y' = e^x(sin(x) + cos(x))

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể tham khảo thêm các bài tập sau:

Bài tập trắc nghiệm về đạo hàm
Bài tập tự luận về đạo hàm
Các đề thi thử Toán 11 có chứa câu hỏi về đạo hàm

Kết luận

Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 11 tập 2. Chúc các em học tập tốt!

Giải mục 1 trang 8, 9 SGK Toán 11 tập 2 - Cùng khám phá