Bài 6.10 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 6.10 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Bài 6.10 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về phép biến hình để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
Đề bài
Tìm hàm số \(y = C.{a^x}\) mà đồ thị của nó được biểu diễn dưới đây:
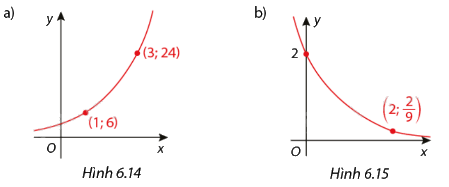
Phương pháp giải - Xem chi tiết
Đồ thị đi qua 2 điểm A(a; b), B (c; d). Thay tọa độ các điểm vào hàm số để tìm C, a.
Lời giải chi tiết
a) Đồ thị hàm số với a >1, đi qua 2 điểm (1; 6) và (3; 24). Ta có:
\(\left\{ \begin{array}{l}C.{a^1} = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\C.{a^3} = 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.a = 6\\{a^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = 2\\a = - 2\,\left( {\rm{L}} \right)\end{array} \right.\\C.a = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\C = 3\end{array} \right.\)
Vậy hàm số cần tìm là \(y = {3.2^x}\).
b) Đồ thị hàm số với 0 < a < 1, đi qua 2 điểm \(\left( {2;\frac{2}{9}} \right)\) và \(\left( {0;2} \right)\). Ta có:
\(\left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C.{a^0} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C.{a^2} = \frac{2}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} = \frac{1}{9}\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = \frac{1}{3}\\a = - \frac{1}{3}\left( {\rm{L}} \right)\end{array} \right.\\C = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{3}\\C = 2\end{array} \right.\)
Vậy hàm số cần tìm là \(y = 2.{\left( {\frac{1}{3}} \right)^x}\)
Bài 6.10 trang 19 SGK Toán 11 tập 2 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 6.10 trang 19 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về phép biến hình. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và tính chất của các phép biến hình cơ bản.
1. Tóm tắt lý thuyết trọng tâm
- Phép tịnh tiến: Biến mỗi điểm thành một điểm sao cho vectơ nối hai điểm đó bằng một vectơ cho trước.
- Phép quay: Biến mỗi điểm thành một điểm sao cho khoảng cách từ điểm đó đến tâm quay không đổi và góc giữa hai đoạn thẳng nối tâm quay với điểm cũ và điểm mới là một góc cho trước.
- Phép đối xứng trục: Biến mỗi điểm thành một điểm sao cho trục đối xứng là đường trung trực của đoạn thẳng nối hai điểm đó.
- Phép đối xứng tâm: Biến mỗi điểm thành một điểm sao cho tâm đối xứng là trung điểm của đoạn thẳng nối hai điểm đó.
2. Phân tích đề bài Bài 6.10 trang 19 SGK Toán 11 tập 2
Đề bài yêu cầu chúng ta xác định phép biến hình thích hợp để biến một hình cho trước thành một hình khác. Để làm được điều này, chúng ta cần phân tích kỹ các yếu tố của hai hình, như vị trí, kích thước, hình dạng và hướng.
3. Giải chi tiết Bài 6.10 trang 19 SGK Toán 11 tập 2
(Nội dung giải bài tập cụ thể sẽ được trình bày chi tiết tại đây, bao gồm các bước thực hiện, công thức sử dụng và kết quả cuối cùng. Ví dụ: Giả sử đề bài yêu cầu tìm phép tịnh tiến biến điểm A(xA, yA) thành điểm A'(xA', yA'). Ta sẽ tính vectơ tịnh tiến v = (xA' - xA, yA' - yA) và viết phương trình của phép tịnh tiến.)
4. Ví dụ minh họa và bài tập tương tự
Để giúp học sinh hiểu rõ hơn về cách giải bài tập về phép biến hình, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự. Ví dụ:
- Tìm phép quay tâm O góc 90° biến điểm M(1, 2) thành điểm M'.
- Tìm phép đối xứng trục Ox biến điểm N(-3, 4) thành điểm N'.
5. Mở rộng và nâng cao
Ngoài việc giải các bài tập trong SGK, học sinh có thể tìm hiểu thêm về các ứng dụng của phép biến hình trong thực tế, như trong thiết kế đồ họa, kiến trúc, và các lĩnh vực khoa học khác. Việc nắm vững kiến thức về phép biến hình sẽ giúp học sinh giải quyết các bài toán phức tạp hơn và phát triển tư duy logic.
6. Lời khuyên khi học tập
Để học tốt môn Toán 11, đặc biệt là phần phép biến hình, học sinh cần:
- Nắm vững các định nghĩa, tính chất và công thức liên quan.
- Luyện tập thường xuyên các bài tập từ cơ bản đến nâng cao.
- Tìm hiểu các ứng dụng thực tế của kiến thức đã học.
- Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải Bài 6.10 trang 19 SGK Toán 11 tập 2 và đạt kết quả tốt trong môn học.