Giải câu hỏi trang 48, 49 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải Câu Hỏi Toán 11 Tập 2 Trang 48, 49
Tusach.vn xin giới thiệu bộ giải đáp chi tiết các bài tập trang 48, 49 sách giáo khoa Toán 11 tập 2. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Mục tiêu của chúng tôi là cung cấp cho bạn những lời giải chính xác, dễ hiểu, cùng với các phương pháp giải hiệu quả, giúp bạn củng cố kiến thức và tự tin hơn trong quá trình học tập.
Dân số của thành phố A tăng theo từng năm kể từ năm 2000 đến nay.
Bài toán 1
Dân số của thành phố A tăng theo từng năm kể từ năm 2000 đến nay. Giả sử số dân của thành phố trên được ước tính bởi công thức \(f\left( t \right) = \frac{{30t + 18}}{{t + 6}}\) (nghìn người), trong đó \(t\) là số năm kể từ năm \(2000\). Chẳng hạn, ở thời điểm năm 2020 thì \(t = 2020 - 2000 = 20\).
a) Nếu xem \(y = f\left( t \right)\) là hàm số xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\) thì đạo hàm của nó biểu thị cho đại lượng nào?
b) Tính tốc độ tăng dân số của thành phố A vào năm 2005 và 2010 (làm tròn kết quả đến hàng phần trăm). Vào năm nào trong hai năm nêu trên, dân số của thành phố A tăng nhanh hơn?
c) Vào năm nào thì tốc độ tăng dân số đạt mức 0,5 nghìn người/năm?
Phương pháp giải:
a) Áp dụng \(s'\left( t \right) = v\left( t \right)\) nên \(f'\left( t \right)\) sẽ biểu thị cho tốc độ tăng dân số.
b) Áp dụng công thức tính \(\left( {\frac{u}{v}} \right)' = \frac{{u'.v - v'.u}}{{{v^2}}}\)
Thay \(t\) tìm được vào \(f'\left( t \right)\) là ta tìm được tốc độ tăng dân số của thành phố A vào năm đó
c) Giải phương trình \(f'\left( t \right) = 0,5\)
Lời giải chi tiết:
a) \(f'\left( t \right)\) biểu thị cho tốc độ tăng dân số của thành phố A
b) Ta có \(f'\left( t \right) = \frac{{\left( {30t + 18} \right)'.\left( {t + 6} \right) - \left( {t + 6} \right)'.\left( {30t + 18} \right)}}{{{{\left( {t + 6} \right)}^2}}} = \frac{{30\left( {t + 6} \right) - \left( {30t + 18} \right)}}{{{{\left( {t + 6} \right)}^2}}} = \frac{{162}}{{{{\left( {t + 6} \right)}^2}}}\)
+) Với năm \(2005\) thì \(t = 2005 - 2000 = 5\).
Suy ra tốc độ tăng dân số là \(f'\left( 5 \right) = \frac{{162}}{{{{\left( {5 + 6} \right)}^2}}} = \frac{{162}}{{121}} \approx 1,34\)nghìn người/năm
+) Với năm 2010 thì \(t = 2010 - 2000 = 10\)
Suy ra tốc độ tăng dân số là \(f'\left( {10} \right) = \frac{{162}}{{{{\left( {10 + 6} \right)}^2}}} \approx 0,63\)nghìn người/năm
c) Để tốc độ tăng dân số đạt mức \(0,5\) nghìn người/năm là
\(f'\left( t \right) = 0,5 \Leftrightarrow \frac{{162}}{{{{\left( {t + 6} \right)}^2}}} = 0,5 \Leftrightarrow {\left( {t + 6} \right)^2} = 324 \Leftrightarrow t + 6 = 18 \Leftrightarrow t = 12\)
Vậy năm \(2012\) thì tốc độ tăng dân số đạt mức \(0,5\) nghìn người/năm
Bài toán 2
Một bể chứa nước đang chứa \(20{m^3}\) nước. Một người cần lấy nước để sử dụng nên đã mở van ở đáy bể để nước chảy vào thùng chứa. Giả sử thể tích nước trong thùng chứa tăng dần theo thời gian và được ước tính bởi hàm số \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\,\,\,\left( {0 \le t \le 40} \right)\).
a) Có thể xem tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng. Tính tốc độ nước chảy vào thùng chứa tại thời điểm \(t = 5\) phút và \(t = 15\) phút.
b) Nước chảy vào thùng chứa nhanh nhất tại thời điểm nào?
Phương pháp giải:
a) Vì tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng nên tốc độ nước chảy vào thùng là \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\)
b) Biến đổi \(V\left( t \right)\) về dạng bình phương
Lời giải chi tiết:
a) Vì tốc độ nước chảy vào thùng bằng với tốc độ tăng của thể tích nước trong thùng nên tốc độ nước chảy vào thùng là \(V\left( t \right) = t - \frac{1}{{80}}{t^2}\)
\(V\left( 5 \right) = 5 - \frac{1}{{80}}{.5^2} = 4,6875\) \({m^3}\)/phút
\(V\left( {15} \right) = 15 - \frac{1}{{80}}{.15^2} = 12,1875\)\({m^3}\)/phút
b) Ta có \(V\left( t \right) = - \frac{1}{{80}}\left( {{t^2} - 80t} \right) = - \frac{1}{{80}}{\left( {t - 40} \right)^2} + 20 \le 20\)
Dấu “=” xảy ra khi và chỉ khi \(t - 40 = 0 \Leftrightarrow t = 40\)
Vậy tại thời điểm \(t = 40\) thì nước chảy vào thùng nhanh nhất
Bài toán 3
Để đo lường khả năng nắm vững kiến thức của sinh viên sau khi kết thức khóa học, một nhà nghiên cứu tiến hành cho sinh viên làm bài kiểm tra mỗi tháng trong vòng 12 tháng kể từ ngày kết thức khóa học. Giả sử điểm số trung bình \(s\left( t \right)\) của các sinh viên đạt được trong bài kiểm tra ở tháng thứ \(t\) được tính bởi \(s\left( t \right) = 7.{e^{ - 0,2t}} + 1\) với \(s\left( t \right)\) tính bằng điểm, \(0 \le t \le 12\). Nếu xem \(y = s\left( t \right)\) là hàm số xác định trên \(\left[ {0;12} \right]\) thì \(\left| {s'\left( t \right)} \right|\) biểu thị tốc độ giẩm điểm số tại tháng thứ \(t\) trong đợt khảo sát.
Tính tốc độ giảm điểm số tại \(t = 2\) và \(t = 6\). Tại thời điểm nào trong hai thời điểm trên, điểm số của các sinh viên được khảo sát giảm nhanh hơn?
Phương pháp giải:
Tính đạo hàm của hàm số \(s\left( t \right)\).
Áp dụng công thức \(\left( {{e^u}} \right)' = u'.{e^u}\)
Thay \(t = 2;t = 6\) vào \(\left| {s'\left( t \right)} \right|\) ta tìm được tốc độ giảm điểm số
Lời giải chi tiết:
Ta có \(s'\left( t \right) = \left( {7{e^{ - 0,2t}} + 1} \right)' = 7.{e^{ - 0,2t}}.\left( { - 0,2t} \right)' = - 1,4.{e^{ - 0,2t}}\)
\( \Rightarrow \left| {s'\left( t \right)} \right| = 1,4.{e^{ - 0,2t}}\) là tốc độ giảm điểm số tại tháng thứ \(t\)
+) Với \(t = 2\) thì tốc độ giảm điểm số là \(1,4.{e^{ - 0,2.2}} \approx 0,9384\)
+) Với \(t = 6\) thì tốc độ giảm điểm số là \(1,4.{e^{ - 0,2.6}} \approx 0,4217\)
Vậy tại thời điểm \(t = 2\) thì điểm số của sinh viên được khảo sát giảm nhanh hơn
Bài toán 4
Cân nặng của một bé gái trong độ tuổi từ 0 đến 36 tháng được ước tính bởi hàm số \(y = f\left( t \right) = 0,00031{t^3} - 0,02396{t^2} + 0,76806t + 3,3\) và có đồ thị như sau (nguồn: https://www.vinmec.com):
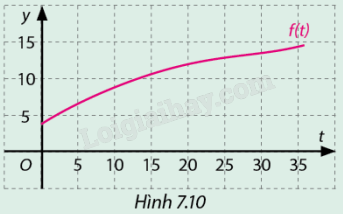
a) Tính tốc độ tăng cân nặng của bé gái tại thời điểm 5 tháng tuổi.
b) Trong ba thời điểm \(t = 5;t = 10;t = 15\), thời điểm nào cân nặng bé gái tăng nhanh nhất?
Phương pháp giải:
a) Tốc độ tăng cân nặng chính là đạo hàm của hàm \(f\left( t \right)\)
b) Thay \(t = 5;t = 10;t = 15\) vào đạo hàm của hàm \(f\left( t \right)\)
Lời giải chi tiết:
a) Tốc độ tăng cân nặng là \(f'\left( t \right) = 0,00093{t^2} - 0,04792t + 0,76806\)
Vậy tốc tăng cân nặng của bé gái tại thời điểm \(5\) tháng tuổi là
\(f'\left( 5 \right) = 0,55171\)
b) Tại thời điểm \(t = 5\) là \(f'\left( 5 \right) = 0,55171\)
Tại thời điểm \(t = 10\) là \(f'\left( {10} \right) = 0,38186\)
Tại thời điểm \(t = 15\) là \(f'\left( {15} \right) = 0,25851\)
Vậy tại thời điểm \(t = 5\) tháng là cân nặng của bé gái tăng nhanh nhất.
Giải Chi Tiết Bài Tập Toán 11 Tập 2 Trang 48, 49
Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 trang 48, 49 của Tusach.vn. Trang này tập trung vào các bài tập thuộc chương trình học, thường liên quan đến các chủ đề như phép biến hình, hàm số lượng giác, hoặc các ứng dụng của đạo hàm. Chúng tôi sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết, dễ hiểu, và kèm theo các lưu ý quan trọng để các em có thể nắm vững kiến thức.
Nội Dung Chính Trang 48, 49 Toán 11 Tập 2
Thông thường, trang 48 và 49 SGK Toán 11 tập 2 sẽ chứa các bài tập vận dụng kiến thức đã học vào giải quyết các bài toán thực tế. Các dạng bài tập thường gặp bao gồm:
- Bài tập về phép biến hình: Xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép biến hình cho trước (phép tịnh tiến, phép quay, phép đối xứng).
- Bài tập về hàm số lượng giác: Tìm tập xác định, tập giá trị, chu kỳ, và vẽ đồ thị của hàm số lượng giác.
- Bài tập về đạo hàm: Tính đạo hàm của hàm số, tìm cực trị, và khảo sát hàm số.
- Bài tập ứng dụng: Giải các bài toán liên quan đến thực tế, sử dụng kiến thức về hàm số và đạo hàm.
Lời Giải Chi Tiết Các Bài Tập
Dưới đây là lời giải chi tiết cho từng bài tập trang 48, 49 SGK Toán 11 tập 2:
Bài 1: (Ví dụ minh họa)
Đề bài: Cho điểm A(1; 2). Tìm ảnh của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải: Gọi A'(x'; y') là ảnh của điểm A qua phép tịnh tiến theo vectơ v. Ta có:
- x' = x + vx = 1 + 3 = 4
- y' = y + vy = 2 + (-1) = 1
Vậy A'(4; 1).
Bài 2: (Ví dụ minh họa)
Đề bài: Tìm tập xác định của hàm số y = √(2x - 1).
Lời giải: Hàm số y = √(2x - 1) xác định khi và chỉ khi 2x - 1 ≥ 0. Giải bất phương trình này, ta được x ≥ 1/2. Vậy tập xác định của hàm số là D = [1/2; +∞).
Mẹo Học Toán 11 Tập 2 Hiệu Quả
Để học tốt môn Toán 11 tập 2, các em nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các định nghĩa, định lý, và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và củng cố kiến thức.
- Tìm kiếm sự giúp đỡ khi cần thiết: Đừng ngần ngại hỏi thầy cô, bạn bè, hoặc tìm kiếm trên internet khi gặp khó khăn.
- Sử dụng các nguồn tài liệu hỗ trợ: Sách bài tập, đề thi thử, và các trang web học trực tuyến có thể giúp các em học tập hiệu quả hơn.
Tusach.vn – Đồng Hành Cùng Các Em
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, và lời giải bài tập môn Toán 11 tập 2. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chương | Nội Dung Chính |
|---|---|
| 1 | Phép Biến Hình |
| 2 | Hàm Số Lượng Giác |
| 3 | Đạo Hàm |
| Nội dung chương trình Toán 11 tập 2 | |