Giải mục 4 trang 112, 113, 114 SGK Toán 11 tập 1 - Cùng khám phá

Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( {\alpha'}\right)\). Trên \(\left( \alpha \right)\), lấy tam giác ABC. Qua các đỉnh A, B, C, ta vẽ các đường thẳng song song với nhau và cắt \(\left( {\alpha '} \right)\) lần lượt tại A, B, C. Các tứ giác ABB′A′, BCC′B′, ACC′A′ là hình gì? Hãy nhận xét về hai tam giác ABC và A′B′C′.

Phương pháp giải:

- Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

- Hình bình hành là tứ giác có 2 cặp cạnh đối song song với nhau.

Lời giải chi tiết:

(ABB′A′) cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến AB, A’B’. Suy ra AB // A’B’.

Mà AA’ // BB’ nên ABB′A′ là hình bình hành. Do đó AB = A'B'.

(BCC′B′) cắt cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến BC, B’C’. Suy ra BC // B’C’.

Mà BB’ // CC’ nên BCC′B′ là hình bình hành. Do đó BC = B'C'.

(ACC′A′) cắt 2 mặt phẳng song song \(\left( \alpha \right)\), \(\left( {\alpha '} \right)\) lần lượt theo giao tuyến AC, A’C’. Suy ra AC // A’C’.

Mà AA’ // CC’ nên ACC′A′ là hình bình hành. Do đó AC = A'C'.

Tam giác ABC và tam giác A'B'C' bằng nhau vì AB = A'B', BC = B'C', AC = A'C'.

Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D'. Chứng minh rằng AO song song A'O '.

Phương pháp giải:

Cho 2 mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

Lời giải chi tiết:

(AA'O'O) cắt 2 mặt phẳng song song (ABCD), (A'B'C'D') theo giao tuyến AO, A'O'. Suy ra AO // A'O'.

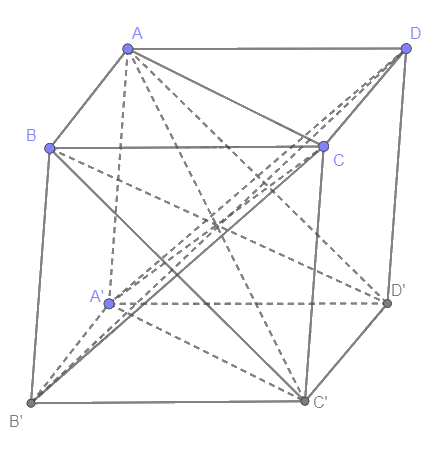
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng bốn đường chéo của hình hộp cắt nhau tại trung điểm của mỗi đường.

Phương pháp giải:

Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.

Lời giải chi tiết:

Ta có ABCD.A'B'C'D' là hình hộp nên AB // C'D' (vì cùng // CD) và AB = C'D' (vì cùng = CD). Suy ra ABC'D' là hình bình hành. Do đó AC' và BD' cắt nhau tại trung điểm của mỗi đường (1)

A'B // CD (vì cùng // AB) và A'B = CD (vì cùng = AB). Suy ra A'BCD là hình bình hành. Do đó A'C và B'D cắt nhau tại trung điểm của mỗi đường (2)

AA' // CC' (vì cùng // BB') và AA' = CC' (vì cùng = BB'). Suy ra ACC'A' là hình bình hành. Do đó AC' và BD' cắt nhau tại trung điểm của mỗi đường (3)

Từ (1), (2), (3) suy ra bốn đường chéo cắt nhau tại trung điểm của mỗi đường.