Giải mục 1 trang 55, 56 SGK Toán 11 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 55, 56 sách giáo khoa Toán 11 tập 2. Bài viết này của tusach.vn sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.

Quan sát hình ảnh cây cột và nền nhà (Hình 8.6). Xem nền nhà là hình ảnh của mặt phẳng \(\left( \alpha \right)\).

Hoạt động 1

Quan sát hình ảnh cây cột và nền nhà (Hình 8.6). Xem nền nhà là hình ảnh của mặt phẳng \(\left( \alpha \right)\). Ta có cạnh \(OO'\) của cây cột tượng trưng cho một đường thẳng với \(O\) tượng trưng cho một điểm thuộc \(\left( \alpha \right)\)

a) Vẽ một đường thẳng \(a\) nằm trong \(\left( \alpha \right)\) và \(a\) không đi qua \(O\). Vẽ đường thẳng \(a'\) qua \(O\) và song song với \(a\). Dùng ê ke kiểm tra \(OO'\) có vuông góc với đường thẳng \(a'\) hay không? Từ đó hãy tính góc giữa \(OO'\) và \(a\).

b) Gọi \(d\) là đường thẳng bất kì nằm trong \(\left( \alpha \right)\). Hỏi \(OO'\) có vuông góc với \(d\) không? Vì sao?

Giải mục 1 trang 55, 56 SGK Toán 11 tập 2 - Cùng khám phá 1

Phương pháp giải:

Để dùng eke kiểm tra vuông góc ta đặt cạnh của eke trùng với \(OO'\), nếu cạnh eke còn lại trùng với đường thẳng \(a\) thì \(OO'\) vuông góc với \(a\)

Lời giải chi tiết:

a) \(OO'\) có vuông góc với đường thẳng \(a\). Góc giữa \(OO'\) và đường thẳng \(a\) bằng \({90^o}\)

b) \(OO'\) vuông góc với \(d\) vì \(OO'\) vuông góc với \(\left( \alpha \right)\)

Luyện tập 1

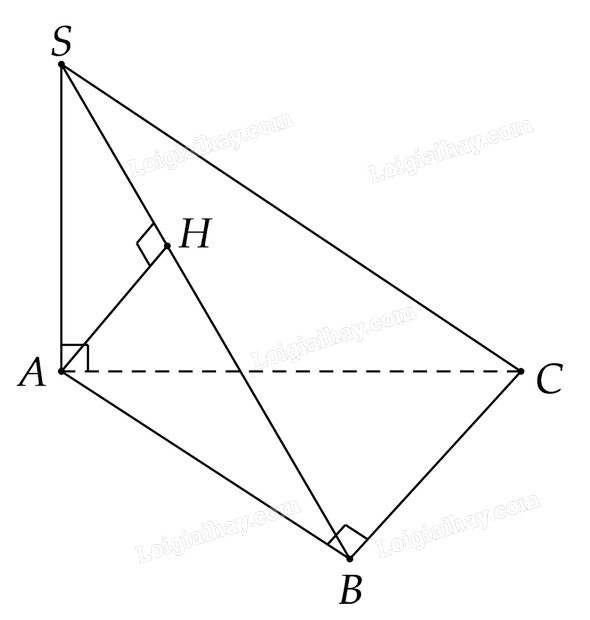
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và tam giác \(ABC\) vuông tại \(B\).

a) Chứng minh rằng \(BC\) vuông góc với mặt phẳng \(\left( {SAB} \right)\)

b) Biết \(AH\) là đường cao của tam giác \(SAB\). Chứng minh \(AH\) vuông góc với \(SC\)

Phương pháp giải:

a) Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

Chứng minh \(BC\) vuông góc với \(SA\) và \(AB\)

b) Chứng minh \(AH\) vuông góc với \(BC\) và \(SB\)

Lời giải chi tiết:

Giải mục 1 trang 55, 56 SGK Toán 11 tập 2 - Cùng khám phá 1

a) Ta có \(BC \bot AB\) vì \(\Delta ABC\) vuông tại \(B\)

Ta có \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)

Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\SA \cap AB = \left\{ A \right\}\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)

b) Ta có \(\left\{ \begin{array}{l}BC \bot \left( {SAB} \right)\\AH \subset \left( {SAB} \right)\end{array} \right. \Rightarrow BC \bot AH\)

Vì \(AH\) là đường cao của tam giác \(SAB\) \( \Rightarrow AH \bot SB\)

Ta có \(\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\)

Giải mục 1 trang 55, 56 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải

Mục 1 trang 55, 56 SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các khái niệm cơ bản, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức trong mục này là vô cùng quan trọng, vì nó là nền tảng cho các kiến thức nâng cao hơn trong chương trình Toán 11 và các chương trình học tiếp theo.

Nội dung chính của Mục 1 trang 55, 56

Khái niệm đạo hàm: Định nghĩa đạo hàm của hàm số tại một điểm, ý nghĩa hình học và vật lý của đạo hàm.
Quy tắc tính đạo hàm: Các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, đạo hàm của hàm hợp.
Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác.
Ứng dụng của đạo hàm: Giải các bài toán tìm cực trị, khoảng đơn điệu của hàm số, bài toán liên quan đến tiếp tuyến của đồ thị hàm số.

Phương pháp giải bài tập hiệu quả

Để giải các bài tập trong mục 1 trang 55, 56 SGK Toán 11 tập 2 một cách hiệu quả, các em cần:

Nắm vững lý thuyết: Hiểu rõ các khái niệm, định lý và quy tắc liên quan đến đạo hàm.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi, phần mềm toán học hoặc các trang web giải toán trực tuyến để kiểm tra kết quả và tìm kiếm lời giải.
Phân tích bài toán: Đọc kỹ đề bài, xác định các yếu tố quan trọng và lựa chọn phương pháp giải phù hợp.

Ví dụ minh họa

Bài tập: Tính đạo hàm của hàm số f(x) = x³ + 2x² - 5x + 1.

Lời giải:

f'(x) = 3x² + 4x - 5

Các dạng bài tập thường gặp

Các bài tập trong mục 1 trang 55, 56 SGK Toán 11 tập 2 thường gặp các dạng sau:

Tính đạo hàm của hàm số.
Tìm đạo hàm cấp hai của hàm số.
Giải phương trình đạo hàm bằng 0 để tìm cực trị của hàm số.
Xác định khoảng đơn điệu của hàm số.
Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm.

Tài liệu tham khảo hữu ích

Ngoài SGK Toán 11 tập 2, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:

Sách bài tập Toán 11 tập 2.
Các trang web giải toán trực tuyến như tusach.vn, loigiaihay.com, vted.vn.
Các video bài giảng trên YouTube.

Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và phương pháp giải bài tập hiệu quả cho mục 1 trang 55, 56 SGK Toán 11 tập 2. Chúc các em học tập tốt!

Giải mục 1 trang 55, 56 SGK Toán 11 tập 2 - Cùng khám phá