Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Mục 4 tập trung vào các bài toán về hàm số, đặc biệt là các dạng bài liên quan đến tính đơn điệu, cực trị và ứng dụng của đạo hàm.
Trong mặt phẳng \(\left( \alpha \right)\), vẽ một hình vuông ABCD, gọi O là giao điểm của AC và BD.
Hoạt động 8
Trong mặt phẳng \(\left( \alpha \right)\), vẽ một hình vuông ABCD, gọi O là giao điểm của AC và BD.
- Qua O, vẽ dường thẳng a vuông góc với \(\left( \alpha \right)\).
- Trên đường thẳng a lấy điểm S khác O. So sánh độ dài các đoạn thẳng SA, SB, SC, SD và rút ra nhận xét về hình dạng các mặt bên của hình chóp S.ABCD.
Phương pháp giải:
Chứng minh tam giác SAC, SBD cân tại S và SA = SB.
Lời giải chi tiết:
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC,SO \bot BD\)
O là giao điểm AC và BD của hình vuông ABCD nên O là trung điểm của AC, BD
Suy ra tam giác SAC cân tại S, tam giác SBD cân tại S
Nên SA = SC, SB = SD
Ta có: \(SA = \sqrt {A{O^2} + S{O^2}} ,SB = \sqrt {B{O^2} + S{O^2}} \)
ABCD là hình vuông nên AO = BO
Suy ra SA = SB = SC = SD.
Luyện tập 6
Cho hình chóp lục giác đều S.ABCDEF có cạnh bên bằng 2a và cạnh đáy bằng a (Hình 8,43). Gọi O là tâm của đáy. Tính SO.

Phương pháp giải:
Đáy là hình lục giác nên AO = a. Áp dụng định lý Py-ta-go để tính SO.
Lời giải chi tiết:
ABCDEF là lục giác đều nên AO = a
Xét tam giác SAO vuông tại O có:
\(SO = \sqrt {S{A^2} + A{O^2}} = \sqrt {{a^2} + {a^2}} = \sqrt 2 a\)
Hoạt động 9
Cho hình chóp tam giác đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh SA, SB, SC (Hình 8,44).
a) Mặt phẳng (A’B’C’) có song song với mặt phẳng (ABC) không? Vì sao?
b) Tam giác A’B’C’ có phải là tam giác đều không? Vì sao?
c) Các tứ giác ABB'A', BCC’B’, ACC’A’ có hình dạng đặc biệt gì?

Phương pháp giải:
a) Nếu mặt phẳng (P) chứa đường thẳng a, b cắt nhau và cùng song song với (Q) thì (P) song song với (Q).
b) Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh đó.
c) Hình thang là tứ giác có 2 cạnh đáy song song với nhau.
Lời giải chi tiết:
a) A’, B’ là trung điểm của SA, SB nên A’B’ song song với AB
A’, C’ là trung điểm của SA, SC nên A’C’ song song với AC
(A’B’C’) song song với (ABC) vì A’B’ song song với AB, A’C’ song song với AC.
b) A’, B’ là trung điểm của SA, SB nên A’B’ = \(\frac{1}{2}\)AB
A’, C’ là trung điểm của SA, SC nên A’C’ = \(\frac{1}{2}\)AC
B’, C’ là trung điểm của SB, SC nên B’C’ = \(\frac{1}{2}\)BC
Mà AB = AC = CA nên A’B’ = A’C’ = C’A’
Vậy A’B’C’ là tam giác đều.
c) ABB’A’ là hình thang vì AB song song với A’B’
BCC’B’ là hình thang vì BC song song với B’C’
ACC’A’ là hình thang vì AC song song với A’C’.
Luyện tập 7
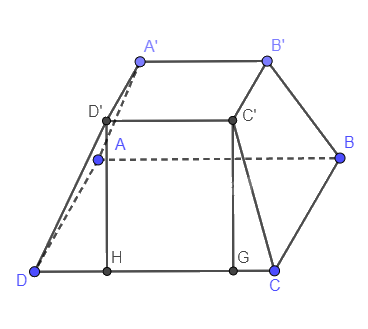
Cho hình chóp cụt tứ giác đều ABCD.AB’C’D’ có cạnh đáy lớn bằng 3a, cạnh đáy nhỏ bằng a, cạnh bên bằng 2a. Tính chiều cao của hình chóp cụt đều này.
Phương pháp giải:
Kẻ C’H, D’G vuông góc với CD. Suy ra C’H song song với D’G. Tính CH và áp dụng định lý Py-ta-go để tính C’H.
Lời giải chi tiết:

Kẻ D’H, C’G vuông góc với CD. Suy ra D’H song song với C’G
Mà C’D’ song song với CD
Suy ra D’C’GH là hình chữ nhật
\( \Rightarrow HG = C'G' = a\)
\( \Rightarrow DH + GC = 2a \Rightarrow DH = GC = a\)
Xét tam giác D’HD vuông tại H có:
\(D'H = \sqrt {DD{'^2} - D{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt 3 a\)
Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2: Tổng quan và hướng dẫn chi tiết
Mục 4 của SGK Toán 11 tập 2 là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Nắm vững các khái niệm và kỹ năng trong mục này sẽ giúp các em giải quyết các bài toán phức tạp hơn trong các kỳ thi sắp tới.
Nội dung chính của mục 4
- Bài 1: Khảo sát hàm số bậc ba. Bài tập này yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.
- Bài 2: Ứng dụng đạo hàm để giải các bài toán thực tế. Các bài toán này thường liên quan đến việc tối ưu hóa một đại lượng nào đó, ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số.
- Bài 3: Khảo sát hàm số phân thức. Bài tập này yêu cầu học sinh xác định tiệm cận đứng, tiệm cận ngang và vẽ đồ thị hàm số.
- Bài 4: Các bài tập tổng hợp về hàm số và đạo hàm.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 4:
Bài 1: Khảo sát hàm số bậc ba
- Bước 1: Xác định tập xác định của hàm số.
- Bước 2: Tính đạo hàm bậc nhất của hàm số.
- Bước 3: Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị.
- Bước 4: Lập bảng biến thiên của hàm số.
- Bước 5: Vẽ đồ thị hàm số.
Bài 2: Ứng dụng đạo hàm để giải các bài toán thực tế
Để giải các bài toán thực tế bằng đạo hàm, các em cần:
- Xây dựng hàm số biểu diễn đại lượng cần tối ưu hóa.
- Tính đạo hàm của hàm số.
- Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị.
- Kiểm tra điều kiện của bài toán để tìm giá trị lớn nhất hoặc giá trị nhỏ nhất.
Bài 3: Khảo sát hàm số phân thức
Khi khảo sát hàm số phân thức, các em cần chú ý đến:
- Tìm tiệm cận đứng bằng cách giải phương trình mẫu số bằng 0.
- Tìm tiệm cận ngang bằng cách tính giới hạn của hàm số khi x tiến tới vô cùng.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
Lưu ý khi giải bài tập
Để giải bài tập trong mục 4 một cách hiệu quả, các em cần:
- Nắm vững các khái niệm và định lý về hàm số và đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng các em học Toán 11
Tusach.vn tự hào là một nguồn tài liệu học tập uy tín và chất lượng, cung cấp đầy đủ các lời giải chi tiết, bài giảng hay và các tài liệu tham khảo hữu ích cho học sinh lớp 11. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Bài tập | Mức độ khó | Lời giải |
|---|---|---|
| Bài 1 | Trung bình | Xem lời giải |
| Bài 2 | Khó | Xem lời giải |