Bài 4.2 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Bài 4.2 trang 94 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ và các tính chất của chúng.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
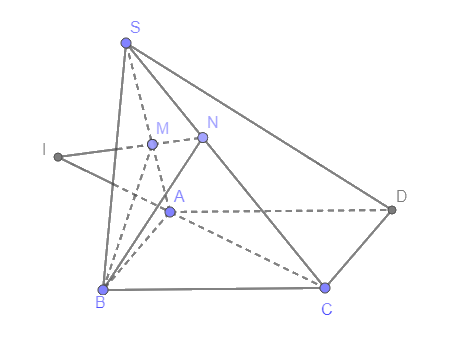
Trong mặt phẳng (P), cho hình bình hành ABCD. Lấy S nằm ngoài mặt phẳng (P). Lấy M, N lần lượt là các điểm nằm trên các cạnh SA, SC.
Bài 4.2 Trang 94 SGK Toán 11 Tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 4.2 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về vectơ và các phép toán liên quan. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 4.2 yêu cầu học sinh thực hiện các phép toán với vectơ, thường bao gồm:
- Tìm vectơ tổng, hiệu của hai vectơ.
- Tìm tích của một số với một vectơ.
- Chứng minh đẳng thức vectơ.
- Giải các bài toán liên quan đến hình học sử dụng vectơ.
Lời giải chi tiết
(Ở đây sẽ là lời giải chi tiết cho bài 4.2 trang 94, ví dụ minh họa)
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: AB + AC = 2AM
Giải:
- Vì M là trung điểm của BC nên BM = MC.
- Ta có: AM = AB + BM
- Và: AM = AC + CM
- Cộng hai đẳng thức trên, ta được: 2AM = AB + BM + AC + CM
- Vì BM = MC nên: 2AM = AB + AC + 2BM
- Do đó: AB + AC = 2AM - 2BM = 2(AM - BM)
- Nhưng AM - BM = BM nên AB + AC = 2AM (đpcm)
Các dạng bài tập tương tự
Ngoài bài 4.2, học sinh có thể gặp các bài tập tương tự như:
- Chứng minh một điểm nằm trên một đường thẳng sử dụng vectơ.
- Tìm tọa độ của một điểm sử dụng vectơ.
- Tính diện tích của một hình đa giác sử dụng vectơ.
Mẹo giải bài tập vectơ
Để giải tốt các bài tập về vectơ, học sinh cần:
- Nắm vững các định nghĩa, tính chất của vectơ.
- Thành thạo các phép toán với vectơ.
- Sử dụng hình vẽ để hỗ trợ việc giải bài tập.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tài liệu tham khảo
Học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
- Sách giáo khoa Toán 11 tập 1.
- Sách bài tập Toán 11 tập 1.
- Các trang web học Toán trực tuyến như tusach.vn.
Kết luận
Bài 4.2 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán 11.