Bài 8.38 trang 89 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.38 trang 89 SGK Toán 11 tập 2
Bài 8.38 thuộc chương trình Toán 11 tập 2, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép đếm và tổ hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các tình huống thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững phương pháp giải và tự tin làm bài tập.
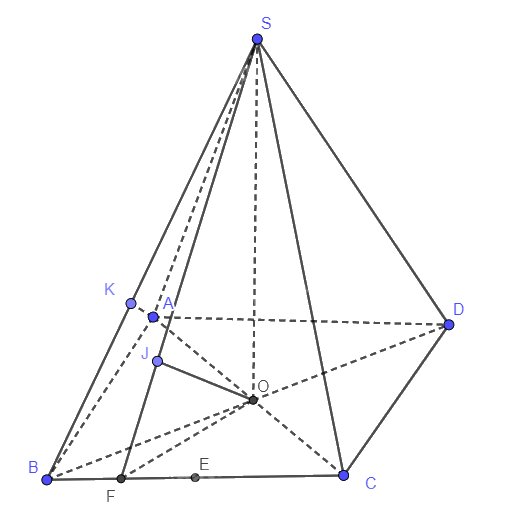
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc BAD = 600.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc BAD = 600. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO = \frac{{3a}}{4}\). Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
Phương pháp giải - Xem chi tiết
a) (P) chứa đường thẳng a vuông góc với (Q) thì (P) và (Q) vuông góc với nhau.
b) Tính khoảng cách từ M đến (P)
+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.
+ Tìm M hạ MH vuông góc với d (H thuộc d).
+ Khi đó MH là khoảng cách cần tìm.
Lời giải chi tiết
a) SO vuông góc với (ABCD) nên SO vuông góc với BC (1)
Ta có: ABCD là hình thoi, góc BAD = 600 nên tam giác ABD đều. Suy ra BD = a
Nên BO =\(\frac{1}{2}a\)
Mà: BE = \(\frac{1}{2}a\), góc CBD = 600
Suy ra tam giác BOE đều
Mà F là trung điểm của BE. Nên OF vuông góc với BC (2)
Từ (1) và (2) suy ra BC vuông góc với (SOF)
Vậy (SBC) vuông góc với (SOF).
b) Ta có: (SBC) vuông góc với (SOF)
SF là giao tuyến của (SOF) và (SBC)
Kẻ OJ vuông góc với SF
Suy ra OJ là khoảng cách từ O đến (SBC)
F là trung điểm BE nên BF = \(\frac{1}{4}a\)
\(OF = \sqrt {O{B^2} - B{F^2}} = \sqrt {{{\left( {\frac{1}{2}a} \right)}^2} - {{\left( {\frac{1}{4}a} \right)}^2}} = \frac{{\sqrt 3 }}{4}a\)
\(\begin{array}{l}\frac{1}{{O{J^2}}} = \frac{1}{{O{F^2}}} + \frac{1}{{S{O^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{4}a} \right)}^2}}} + \frac{1}{{{{\left( {\frac{3}{4}a} \right)}^2}}}\\ \Rightarrow JO = \frac{3}{8}a\end{array}\)
(SAB) và (SBC) vuông góc
Kẻ AK vuông góc với SB nên AK là khoảng cách từ A đến (SBC)
Bài 8.38 Trang 89 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích
Bài 8.38 trang 89 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về tổ hợp và xác suất. Bài tập này thường yêu cầu học sinh tính số lượng các kết quả có thể xảy ra trong một tình huống cụ thể, hoặc tính xác suất của một sự kiện nào đó.
Nội dung bài toán 8.38 trang 89 SGK Toán 11 tập 2
Để hiểu rõ hơn về bài toán, chúng ta cần xem xét nội dung cụ thể của nó. (Giả sử bài toán yêu cầu tính số cách chọn 3 học sinh từ một lớp 20 học sinh để thành lập một tổ):
"Một lớp có 20 học sinh, trong đó có 12 nam và 8 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh để thành lập một tổ trực cờ, trong đó có ít nhất một học sinh nam?"
Phương pháp giải bài toán 8.38 trang 89 SGK Toán 11 tập 2
Có nhiều phương pháp để giải bài toán này, nhưng phương pháp phổ biến nhất là sử dụng công thức tổ hợp và quy tắc cộng xác suất. Trong trường hợp này, chúng ta có thể giải bài toán bằng cách tính tổng số cách chọn 3 học sinh bất kỳ, sau đó trừ đi số cách chọn 3 học sinh đều là nữ.
- Tính tổng số cách chọn 3 học sinh bất kỳ từ 20 học sinh: Sử dụng công thức tổ hợp chập 3 của 20 phần tử: C203 = 20! / (3! * 17!) = 1140
- Tính số cách chọn 3 học sinh đều là nữ: Sử dụng công thức tổ hợp chập 3 của 8 phần tử: C83 = 8! / (3! * 5!) = 56
- Tính số cách chọn 3 học sinh có ít nhất một học sinh nam: Lấy tổng số cách chọn 3 học sinh bất kỳ trừ đi số cách chọn 3 học sinh đều là nữ: 1140 - 56 = 1084
Lời giải chi tiết bài 8.38 trang 89 SGK Toán 11 tập 2
Vậy, số cách chọn ra 3 học sinh để thành lập một tổ trực cờ, trong đó có ít nhất một học sinh nam là 1084 cách.
Các dạng bài tập tương tự và mẹo giải
Các bài tập tương tự bài 8.38 thường yêu cầu học sinh tính số lượng các kết quả có thể xảy ra trong các tình huống khác nhau, hoặc tính xác suất của một sự kiện nào đó. Để giải các bài tập này, học sinh cần nắm vững các công thức tổ hợp và quy tắc cộng xác suất.
- Nắm vững công thức tổ hợp: Cnk = n! / (k! * (n-k)!)
- Hiểu rõ quy tắc cộng xác suất: P(A hoặc B) = P(A) + P(B) - P(A và B)
- Phân tích kỹ đề bài: Xác định rõ các yếu tố cần tính toán và các điều kiện ràng buộc.
- Sử dụng sơ đồ Venn: Sơ đồ Venn có thể giúp học sinh hình dung rõ hơn về các tập hợp và mối quan hệ giữa chúng.
Tài liệu tham khảo và luyện tập thêm
Để luyện tập thêm và nâng cao kiến thức về tổ hợp và xác suất, học sinh có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 tập 2
- Sách bài tập Toán 11 tập 2
- Các trang web học toán trực tuyến như tusach.vn, loigiaihay.com, vted.vn
Kết luận: Bài 8.38 trang 89 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tổ hợp và xác suất. Bằng cách nắm vững các công thức và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| Cnk | Số tổ hợp chập k của n phần tử |
| P(A) | Xác suất của sự kiện A |