Lý Thuyết Hàm Số Lượng Giác & Đồ Thị - Toán 11

Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cùng khám phá

Lý thuyết Hàm số lượng giác và đồ thị - Nền tảng Toán 11

Hàm số lượng giác đóng vai trò quan trọng trong chương trình Toán 11, là nền tảng cho các kiến thức nâng cao hơn.

Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết về lý thuyết hàm số lượng giác, giúp bạn hiểu rõ các khái niệm, tính chất và ứng dụng của chúng.

Cùng khám phá thế giới lượng giác một cách dễ dàng và hiệu quả!

I. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

1. Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

Hàm số f(x) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\)

Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = - f(x)\)

* Lưu ý:

Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

2. Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \) 0 sao cho với mọi \(x \in D\) ta có \(x \pm T \in D\) và \(f(x + T) = f(x)\)

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2\(\pi \).

Các hàm số y = tanx, y=cotx tuần hoàn chu kì \(\pi \).

II. Hàm số lượng giác

1. Định nghĩa các hàm số lượng giác

Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là \(\mathbb{R}\).
Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là \(\mathbb{R}\).
Hàm số cho bằng công thức \(y = \frac{{\sin \alpha }}{{\cos \alpha }}\)được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Hàm số cho bằng công thức \(y = \frac{{\cos \alpha }}{{\sin \alpha }}\)được gọi là hàm số côtang, kí hiệu là y = cotx. Tập xác định của hàm số côtang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).

2. Đồ thị của các hàm số lượng giác

a, Hàm số y = sinx

Tập xác định là \(\mathbb{R}\).
Tập giá trị là [-1;1].
Là hàm số lẻ và tuần hoàn chu kì 2\(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

b, Hàm số y = cosx

Tập xác định là \(\mathbb{R}\).
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2\(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
Có đồ thị là một đường hình sin đối xứng qua trục tung.

c, Hàm số y = tanx

Tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Tập giá trị là \(\mathbb{R}\).
Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).
Có đồ thị đối xứng qua gốc tọa độ.

d, Hàm số y = cotx

Tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
Tập giá trị là \(\mathbb{R}\).
Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
Đồng biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), \(k \in \mathbb{Z}\).
Có đồ thị đối xứng qua gốc tọa độ.

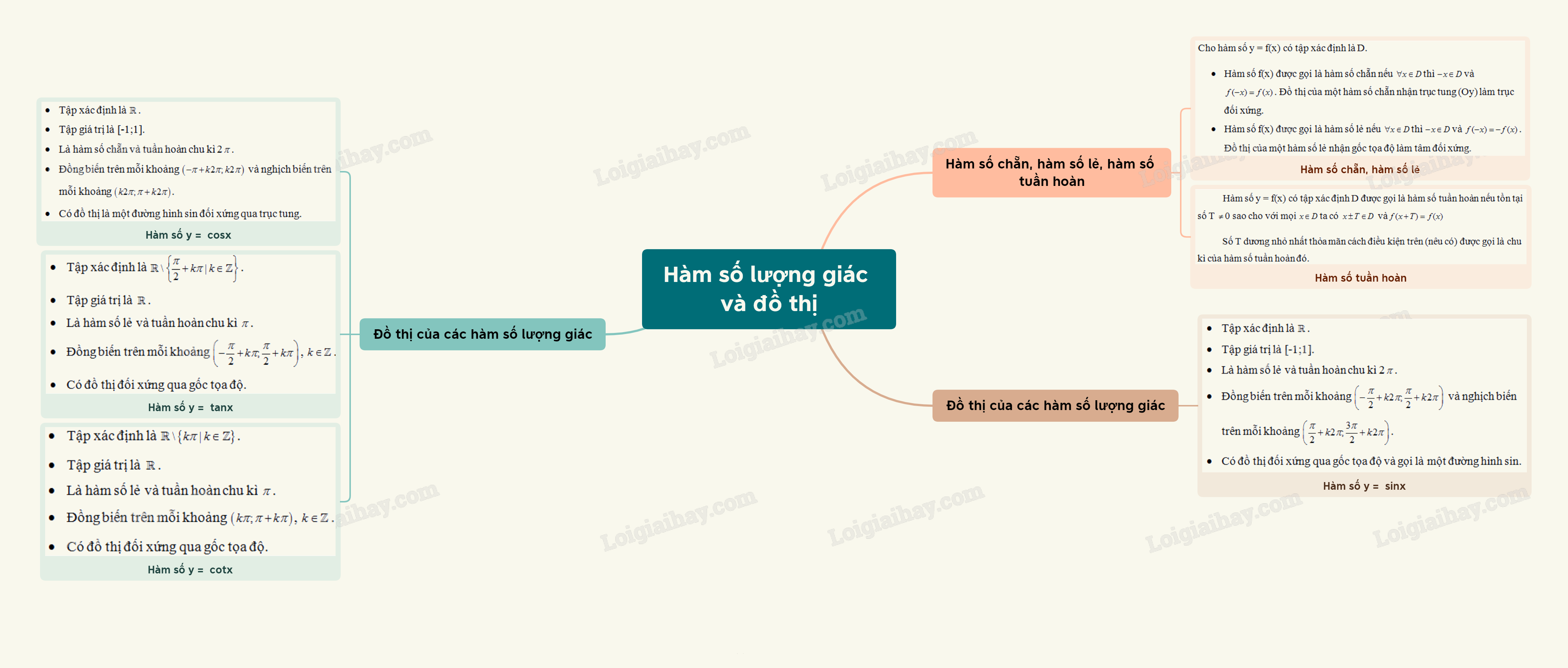
Lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cùng khám phá 1

Lý Thuyết Hàm Số Lượng Giác và Đồ Thị - SGK Toán 11: Tổng Quan và Hướng Dẫn Chi Tiết

Hàm số lượng giác là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 11, đóng vai trò nền tảng cho việc học tập các môn học liên quan đến khoa học tự nhiên và kỹ thuật. Việc nắm vững lý thuyết và kỹ năng giải bài tập về hàm số lượng giác là điều cần thiết để đạt kết quả tốt trong các kỳ thi và ứng dụng vào thực tế.

1. Các Hàm Số Lượng Giác Cơ Bản

Trong chương trình Toán 11, chúng ta thường gặp các hàm số lượng giác cơ bản sau:

Hàm sin (sin x): Được định nghĩa là tỷ số giữa cạnh đối và cạnh huyền trong tam giác vuông.
Hàm cosin (cos x): Được định nghĩa là tỷ số giữa cạnh kề và cạnh huyền trong tam giác vuông.
Hàm tang (tan x): Được định nghĩa là tỷ số giữa cạnh đối và cạnh kề trong tam giác vuông.
Hàm cotang (cot x): Được định nghĩa là tỷ số giữa cạnh kề và cạnh đối trong tam giác vuông.

Mỗi hàm số lượng giác đều có tập xác định, tập giá trị, tính tuần hoàn và các tính chất đặc trưng riêng. Việc hiểu rõ những tính chất này giúp chúng ta giải quyết các bài toán một cách hiệu quả.

2. Đồ Thị Hàm Số Lượng Giác

Đồ thị hàm số lượng giác là biểu diễn hình học của hàm số trên mặt phẳng tọa độ. Việc vẽ và phân tích đồ thị hàm số lượng giác giúp chúng ta hiểu rõ hơn về tính chất của hàm số, tìm ra các điểm đặc biệt như điểm cực trị, điểm đối xứng và các khoảng đồng biến, nghịch biến.

Dưới đây là một số đặc điểm chính của đồ thị các hàm số lượng giác:

Đồ thị hàm sin (y = sin x): Là một đường cong liên tục, tuần hoàn với chu kỳ 2π, nhận gốc tọa độ làm tâm đối xứng.
Đồ thị hàm cosin (y = cos x): Tương tự như đồ thị hàm sin, nhưng bị dịch chuyển sang trái một lượng π/2.
Đồ thị hàm tang (y = tan x): Có các đường tiệm cận đứng tại các điểm x = π/2 + kπ (k là số nguyên).
Đồ thị hàm cotang (y = cot x): Có các đường tiệm cận đứng tại các điểm x = kπ (k là số nguyên).

3. Các Công Thức Lượng Giác Quan Trọng

Việc nắm vững các công thức lượng giác là điều kiện cần thiết để giải quyết các bài toán liên quan đến hàm số lượng giác. Một số công thức lượng giác quan trọng bao gồm:

Công thức	Mô tả
sin²x + cos²x = 1	Công thức lượng giác cơ bản
tan x = sin x / cos x	Mối quan hệ giữa tan, sin và cos
cot x = cos x / sin x	Mối quan hệ giữa cot, sin và cos
sin(a + b) = sin a cos b + cos a sin b	Công thức cộng góc của sin

4. Bài Tập Vận Dụng và Luyện Tập

Để củng cố kiến thức về hàm số lượng giác và đồ thị, bạn nên thực hành giải nhiều bài tập khác nhau. Tusach.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, kèm theo đáp án chi tiết và lời giải thích rõ ràng.

Một số dạng bài tập thường gặp:

Xác định tập xác định, tập giá trị của hàm số lượng giác.
Vẽ đồ thị hàm số lượng giác.
Giải phương trình lượng giác.
Chứng minh đẳng thức lượng giác.
Ứng dụng hàm số lượng giác vào giải quyết các bài toán thực tế.

5. Lời Khuyên Khi Học Hàm Số Lượng Giác

Nắm vững định nghĩa và tính chất của các hàm số lượng giác cơ bản.
Luyện tập vẽ đồ thị hàm số lượng giác thường xuyên.
Học thuộc các công thức lượng giác quan trọng.
Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
Sử dụng các tài liệu học tập chất lượng và đáng tin cậy.

Tusach.vn hy vọng rằng với những thông tin và hướng dẫn chi tiết trên, bạn sẽ có thể nắm vững lý thuyết hàm số lượng giác và đồ thị - SGK Toán 11 một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!