Lý Thuyết Cấp Số Cộng - SGK Toán 11

Lý thuyết Cấp số cộng - SGK Toán 11 Cùng khám phá

Lý Thuyết Cấp Số Cộng - Nền Tảng Toán 11

Cấp số cộng là một trong những khái niệm quan trọng trong chương trình Toán 11, đặc biệt là trong phần Dãy số.

Hiểu rõ lý thuyết về cấp số cộng không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.

Tusach.vn xin giới thiệu bài viết tổng hợp đầy đủ và chi tiết về lý thuyết cấp số cộng, kèm theo các ví dụ minh họa và bài tập thực hành.

1. Cấp số cộng

1. Cấp số cộng

Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d, nghĩa là:

\({u_n} = {u_{n - 1}} + d,n \ge 2\)

Số d được gọi là công sai của cấp số cộng.

* Nhận xét:

- Nếu công sai d = 0 thì mọi số hạng của cấp số cộng đều bằng nhau. Khi đó, cấp số cộng là một dãy số không đổi.

- Nếu \(\left( {{u_n}} \right)\) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:

\({u_k} = \frac{{{u_{k - 1}} + {u_{k + 1}}}}{2}\left( {k \ge 2} \right)\)

II. Số hạng tổng quát

Nếu cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\)của nó được xác định theo công thức\({u_n} = {u_1} + (n - 1)d,n \ge 2.\)

III. Tổng n số hạng đầu của một cấp số cộng

Cho cấp số cộng \(\left( {{u_n}} \right)\)với công sai d. Đặt \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n}\). Khi đó

\({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2} = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right]\)

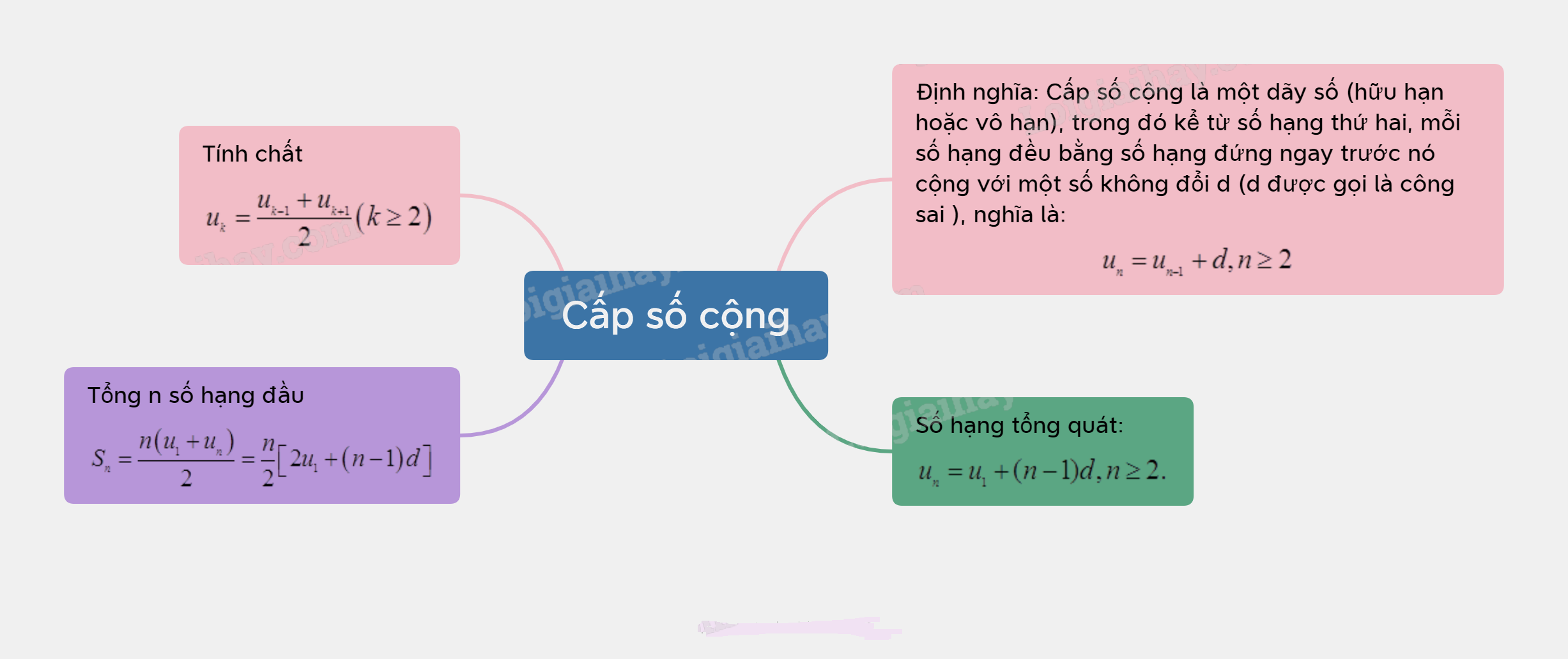
Lý thuyết Cấp số cộng - SGK Toán 11 Cùng khám phá 1

Lý Thuyết Cấp Số Cộng - SGK Toán 11: Tổng Quan

Cấp số cộng là một dãy số mà mỗi số hạng sau được tạo thành bằng cách cộng một số không đổi (gọi là công sai) vào số hạng đứng trước. Đây là một trong những dãy số quan trọng nhất trong toán học, xuất hiện thường xuyên trong nhiều lĩnh vực khác nhau.

1. Định Nghĩa Cấp Số Cộng

Một dãy số (u_n) được gọi là cấp số cộng nếu có một số thực d sao cho:

u_n+1 = u_n + d, với mọi n ≥ 1

Số d được gọi là công sai của cấp số cộng.

2. Các Tính Chất Quan Trọng

Một số tính chất quan trọng của cấp số cộng:

Nếu u₁ là số hạng đầu và d là công sai thì số hạng thứ n của cấp số cộng được tính bởi công thức: u_n = u₁ + (n-1)d
Mọi số hạng của cấp số cộng đều có thể biểu diễn qua số hạng đầu và công sai.
Nếu ba số a, b, c theo thứ tự đó tạo thành một cấp số cộng thì 2b = a + c.

3. Tổng của n Số Hạng Đầu của Cấp Số Cộng

Tổng của n số hạng đầu tiên của một cấp số cộng (S_n) được tính theo công thức:

S_n = (n/2) * (u₁ + u_n) hoặc S_n = (n/2) * [2u₁ + (n-1)d]

4. Ví Dụ Minh Họa

Ví dụ 1: Cho cấp số cộng có số hạng đầu u₁ = 2 và công sai d = 3. Tìm số hạng thứ 5 và tổng của 5 số hạng đầu tiên.

Giải:

u₅ = u₁ + (5-1)d = 2 + 4*3 = 14
S₅ = (5/2) * (u₁ + u₅) = (5/2) * (2 + 14) = 40

Ví dụ 2: Tìm x để các số x, x+1, x+3 tạo thành một cấp số cộng.

Giải:

Áp dụng tính chất 2b = a + c, ta có: 2(x+1) = x + (x+3) => 2x + 2 = 2x + 3 => 2 = 3 (vô lý). Vậy không có giá trị x nào thỏa mãn.

5. Bài Tập Thực Hành

Dưới đây là một số bài tập để bạn luyện tập:

Tìm số hạng thứ 10 của cấp số cộng có u₁ = 1 và d = 2.
Tìm công sai của cấp số cộng có u₂ = 5 và u₅ = 11.
Tính tổng của 20 số hạng đầu tiên của cấp số cộng có u₁ = 3 và d = -1.

6. Ứng Dụng của Cấp Số Cộng

Cấp số cộng có nhiều ứng dụng trong thực tế, ví dụ:

Tính số tiền tiết kiệm theo thời gian với lãi suất cố định.
Tính chiều dài các cạnh của một hình vuông hoặc hình chữ nhật khi tăng dần theo một quy luật nhất định.
Mô tả sự tăng trưởng dân số hoặc số lượng sản phẩm theo thời gian.

7. Lời Khuyên Khi Học Lý Thuyết Cấp Số Cộng

Để nắm vững lý thuyết cấp số cộng, bạn nên:

Hiểu rõ định nghĩa và các tính chất cơ bản.
Luyện tập nhiều bài tập để làm quen với các dạng bài khác nhau.
Sử dụng các công thức một cách linh hoạt và chính xác.
Tìm hiểu các ứng dụng thực tế của cấp số cộng để hiểu rõ hơn về tầm quan trọng của nó.

Tusach.vn hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết cấp số cộng. Chúc bạn học tập tốt!