Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Cùng khám phá
Tổng quan nội dung
Lý thuyết Giá trị lượng giác của góc lượng giác - Toán 11
Bài học này thuộc chương trình SGK Toán 11, tập trung vào việc tìm hiểu các giá trị lượng giác của các góc lượng giác đặc biệt và các công thức liên quan.
Nắm vững lý thuyết này là nền tảng quan trọng để giải quyết các bài toán lượng giác phức tạp hơn trong chương trình học và các kỳ thi.
tusach.vn cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
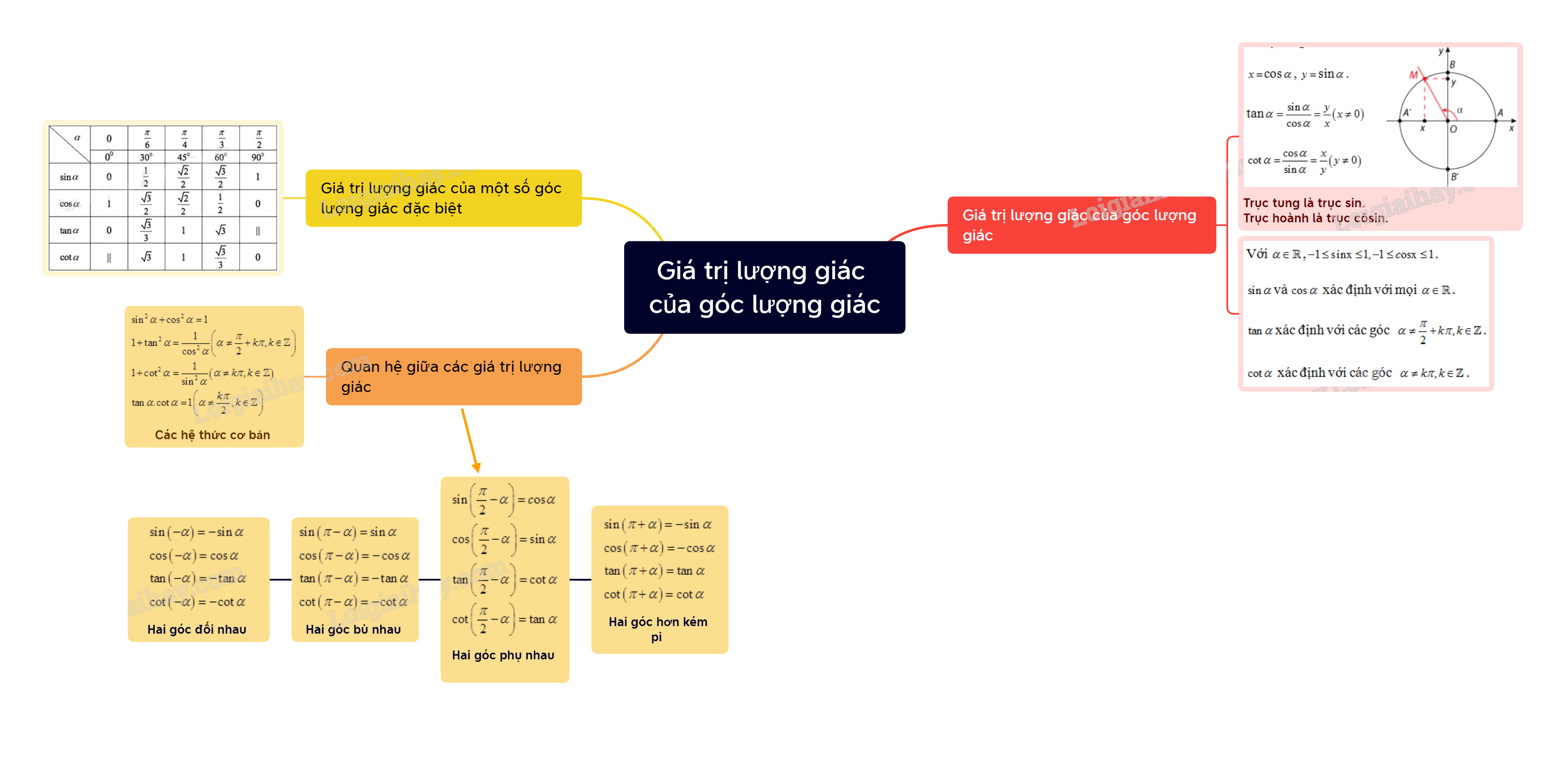
I. Giá trị lượng giác của góc lượng giác
I. Giá trị lượng giác của góc lượng giác
1. Định nghĩa
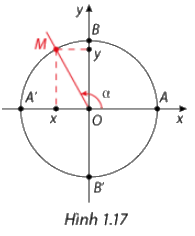
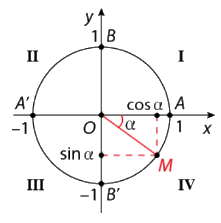
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
- Các giá trị sin\(\alpha \), cos\(\alpha \), tan\(\alpha \), cot\(\alpha \) được gọi là các giá trị lượng giác của góc lượng giác \(\alpha \).
*Chú ý:
a, Trục tung là trục sin, trục hoành là trục côsin.
b, Với \(\alpha \in \mathbb{R}\),\( - 1 \le {\mathop{\rm s}\nolimits} {\rm{inx}} \le 1, - 1 \le c{\rm{osx}} \le 1\).
\(\sin \alpha \)và \(\cos \alpha \) xác định với mọi \(\alpha \in \mathbb{R}\).
\(\tan \alpha \) xác định với các góc \(\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
\(\cot \alpha \) xác định với các góc \(\alpha \ne k\pi ,k \in \mathbb{Z}\).
c, Với mọi góc lượng giác \(\alpha \) và số nguyên k, ta có:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha + k\pi } \right) = \cot \alpha \end{array}\)
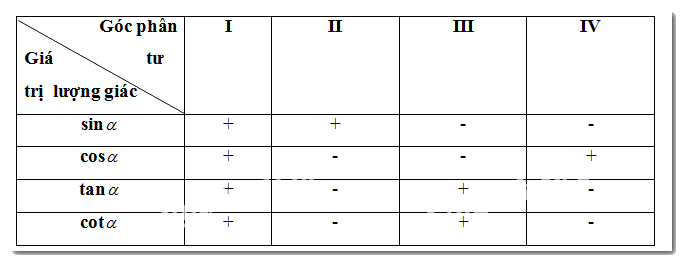
d, Bảng xác định dấu của các giá trị lượng giác
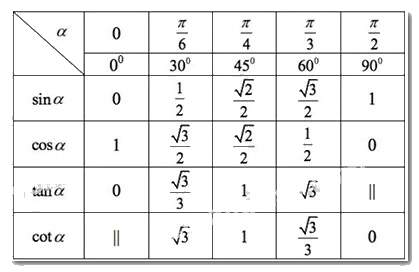
2. Giá trị lượng giác của một số góc lượng giác đặc biệt
3. Sử dụng máy tính cầm tay để tính các giá trị lượng giác của một góc
- Lần lượt ấn các phím SHIFT \( \to \)MENU \( \to \)2 (CASIO 580VN)
Để chọn đơn vị độ: ấn phím 1 (Degree).
Để chọn đơn vị radian: ấn phím 2 (Radian).
- Ấn các phím MENU 1 để vào chế độ tính toán.
II. Quan hệ giữa các giá trị lượng giác
1. Các hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
2. Quan hệ giữa các giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
- Hai góc đối nhau \(\alpha \) và \( - \alpha \)
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc bù nhau (\(\alpha \) và \(\pi \)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
- Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}\)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
- Hai góc hơn kém \(\pi \)(\(\alpha \) và \(\pi \) + \(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
Lý Thuyết Giá Trị Lượng Giác của Góc Lượng Giác - SGK Toán 11: Tổng Quan và Ứng Dụng
Chào mừng các em học sinh đến với bài học về Lý thuyết Giá trị lượng giác của góc lượng giác trong chương trình SGK Toán 11. Đây là một phần kiến thức quan trọng, nền tảng cho việc giải quyết các bài toán liên quan đến lượng giác trong suốt quá trình học tập.
1. Góc Lượng Giác và Số Đo Cung
Trước khi đi sâu vào giá trị lượng giác, chúng ta cần hiểu rõ về góc lượng giác và số đo cung. Một góc lượng giác được xác định bởi một đường tròn lượng giác và một điểm trên đường tròn đó. Số đo cung là độ dài cung trên đường tròn đơn vị, thường được đo bằng radian hoặc độ.
- Độ: Một vòng tròn đầy đủ là 360 độ.
- Radian: Một vòng tròn đầy đủ là 2π radian.
Công thức chuyển đổi giữa độ và radian: radian = (độ * π) / 180
2. Giá Trị Lượng Giác của Góc Lượng Giác
Giá trị lượng giác của một góc lượng giác α (ký hiệu là sin α, cos α, tan α, cot α) được định nghĩa dựa trên tọa độ của điểm M trên đường tròn lượng giác tương ứng với góc α.
- Sin α: Tung độ của điểm M.
- Cos α: Hoành độ của điểm M.
- Tan α: sin α / cos α (xác định khi cos α ≠ 0).
- Cot α: cos α / sin α (xác định khi sin α ≠ 0).
3. Giá Trị Lượng Giác của Các Góc Đặc Biệt
Việc nắm vững giá trị lượng giác của các góc đặc biệt là rất quan trọng. Dưới đây là bảng giá trị lượng giác của một số góc thường gặp:
| Góc (α) | 0° (0 rad) | 30° (π/6 rad) | 45° (π/4 rad) | 60° (π/3 rad) | 90° (π/2 rad) |
|---|---|---|---|---|---|
| sin α | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos α | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan α | 0 | 1/√3 | 1 | √3 | Không xác định |
| cot α | Không xác định | √3 | 1 | 1/√3 | 0 |
4. Các Công Thức Lượng Giác Cơ Bản
Có rất nhiều công thức lượng giác giúp chúng ta biến đổi và tính toán các giá trị lượng giác. Một số công thức quan trọng bao gồm:
- sin2 α + cos2 α = 1
- tan α = sin α / cos α
- cot α = cos α / sin α
- 1 + tan2 α = 1/cos2 α
- 1 + cot2 α = 1/sin2 α
5. Ứng Dụng của Lý Thuyết Giá Trị Lượng Giác
Lý thuyết giá trị lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Giải tam giác: Tính các cạnh và góc của tam giác.
- Vật lý: Mô tả các hiện tượng dao động, sóng.
- Kỹ thuật: Thiết kế các công trình, máy móc.
- Định vị và đo đạc: Xác định vị trí, khoảng cách.
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Giá trị lượng giác của góc lượng giác. Hãy luyện tập thêm các bài tập để củng cố kiến thức và tự tin hơn trong các kỳ thi. Chúc các em học tốt!
Truy cập tusach.vn để xem thêm nhiều tài liệu học tập hữu ích khác.