Bài 8.45 trang 90 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Bài 8.45 trang 90 SGK Toán 11 tập 2
Bài 8.45 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng áp dụng chúng vào việc tìm đạo hàm của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tử diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC.
Đề bài
Cho tử diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC. Gọi M là trung điểm của BC. Góc giữa hai đường thẳng OM và AB bằng
A. 900.
B. 300.
C. 600.
D. 450.
Phương pháp giải - Xem chi tiết
Chọn 2 đường thẳng cắt nhau c và d lần lượt song song với a và b. Khi đó góc giữa c và d là góc giữa a và b.
Lời giải chi tiết
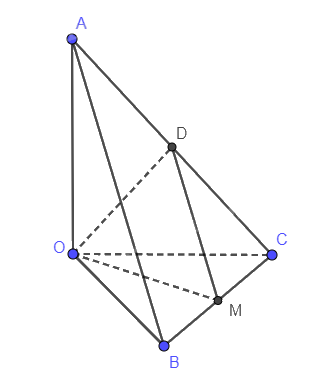
Đặt OA = OB = OC = a
Gọi D là trung điểm của AC nên DM // AB và bằng một nửa AB
\( \Rightarrow \widehat {\left( {OM,AB} \right)} = \widehat {\left( {OM,DM} \right)} = \widehat {OMD}\)
Ta có: OA vuông góc và bằng OC nên tam giác OAC là tam giác vuông cân tại C
\(AC = \sqrt {O{A^2} + O{B^2}} = \sqrt 2 a\)
\(\begin{array}{l}AC.OD = OA.OC\\ \Leftrightarrow OD = \frac{{\sqrt 2 }}{2}a\end{array}\)
Tương tự với OM, ta có: \(OM = \frac{{\sqrt 2 }}{2}a\)
\(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt 2 a\)
Suy ra \(DM = \frac{{\sqrt 2 }}{2}a\)
Vậy tam giác DOM đều. Suy ra \(\widehat {OMD} = {60^0}\).
Chọn đáp án C.
Bài 8.45 Trang 90 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích
Bài 8.45 trang 90 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bài tập này thường yêu cầu học sinh tính đạo hàm của một hàm số hoặc giải một phương trình liên quan đến đạo hàm.
Nội dung bài tập 8.45 trang 90 SGK Toán 11 tập 2
Để hiểu rõ hơn về bài tập này, chúng ta cần xem xét nội dung cụ thể của nó. Thông thường, bài tập sẽ đưa ra một hàm số và yêu cầu tính đạo hàm của hàm số đó tại một điểm cụ thể hoặc trên một khoảng xác định. Ngoài ra, bài tập có thể yêu cầu học sinh sử dụng đạo hàm để giải một bài toán tối ưu hóa hoặc tìm cực trị của hàm số.
Phương pháp giải bài 8.45 trang 90 SGK Toán 11 tập 2
Để giải bài tập 8.45 trang 90 SGK Toán 11 tập 2 một cách hiệu quả, học sinh cần nắm vững các bước sau:
- Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm.
- Chọn công thức đạo hàm phù hợp: Dựa vào dạng của hàm số, chọn công thức đạo hàm phù hợp để tính đạo hàm. Ví dụ, nếu hàm số là một đa thức, ta sử dụng công thức đạo hàm của đa thức. Nếu hàm số là một hàm lượng giác, ta sử dụng công thức đạo hàm của hàm lượng giác.
- Tính đạo hàm: Áp dụng công thức đạo hàm đã chọn để tính đạo hàm của hàm số.
- Kiểm tra kết quả: Kiểm tra lại kết quả tính đạo hàm để đảm bảo tính chính xác.
Ví dụ minh họa giải bài 8.45 trang 90 SGK Toán 11 tập 2
Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x + 1. Ta thực hiện như sau:
- Bước 1: Xác định hàm số: f(x) = x2 + 2x + 1
- Bước 2: Chọn công thức đạo hàm phù hợp: Sử dụng công thức đạo hàm của đa thức: (xn)' = nxn-1
- Bước 3: Tính đạo hàm: f'(x) = 2x + 2
- Bước 4: Kiểm tra kết quả: Kết quả tính đạo hàm là chính xác.
Lưu ý khi giải bài 8.45 trang 90 SGK Toán 11 tập 2
Để đạt được kết quả tốt nhất khi giải bài tập 8.45 trang 90 SGK Toán 11 tập 2, học sinh cần lưu ý những điều sau:
- Nắm vững các công thức đạo hàm cơ bản: Đây là nền tảng để giải quyết các bài tập về đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ: Nếu gặp khó khăn, học sinh có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán.
- Tham khảo các nguồn tài liệu khác: Ngoài SGK, học sinh có thể tham khảo các sách tham khảo, bài giảng trực tuyến hoặc các trang web học tập để mở rộng kiến thức.
Ứng dụng của đạo hàm trong thực tế
Đạo hàm không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật,... Ví dụ, đạo hàm được sử dụng để tính vận tốc và gia tốc của một vật thể chuyển động, để tìm điểm cực trị của một hàm số chi phí hoặc lợi nhuận, hoặc để tối ưu hóa thiết kế của một sản phẩm.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải bài 8.45 trang 90 SGK Toán 11 tập 2 và nắm vững kiến thức về đạo hàm. Hãy truy cập tusach.vn để xem thêm nhiều bài giải và tài liệu học tập Toán 11 hữu ích khác!