Bài 1.16 trang 19 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 1.16 trang 19 SGK Toán 11 tập 1 - Cùng khám phá
Bài 1.16 thuộc chương trình Toán 11 tập 1, tập trung vào việc nghiên cứu hàm số bậc hai và đồ thị parabol. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa, tính chất của hàm số bậc hai để xác định các yếu tố của parabol và vẽ đồ thị.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập Toán 11 hiệu quả.
Một vận động viên bắn súng nằm trên mặt đất để ngắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 20 m tại một góc ngắm (góc hợp bởi phương bắn và phương ngang).
Đề bài
Một vận động viên bắn súng nằm trên mặt đất để ngắm bắn các mục tiêu khác nhau trên một bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 20 m tại một góc ngắm (góc hợp bởi phương bắn và phương ngang). Nếu tăng góc ngắm đó lên hai lần thì vận động viên bắn trúng một mục tiêu cách mặt đất 45 m. Tính khoảng cách từ vận động viên đến bức tường.
Phương pháp giải - Xem chi tiết
Áp dụng tỉ số lượng giác:
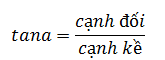
Và công thức nhân đôi.
Lời giải chi tiết
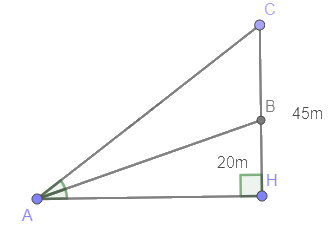
Gọi A là vị trí vận động viên nằm, B là mục tiêu cách mặt đất 20m, C là mục tiêu cách mặt đất 45m và H như trên hình
\(\begin{array}{l}\tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{{20}}{{AH}}\\\tan \widehat {CAH} = \frac{{CH}}{{AH}} = \frac{{45}}{{AH}}\\\widehat {CAH} = 2\widehat {BAH}\\ \Rightarrow \tan \left( {2.\widehat {BAH}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{2\tan \widehat {BAH}}}{{1 - {{\tan }^2}\widehat {BAH}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \left( {2.\frac{{20}}{{AH}}} \right):\left[ {1 - {{\left( {\frac{{20}}{{AH}}} \right)}^2}} \right] = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\left( {1 - \frac{{400}}{{A{H^2}}}} \right) = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}:\frac{{A{H^2} - 400}}{{A{H^2}}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40}}{{AH}}.\frac{{A{H^2}}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow \frac{{40AH}}{{A{H^2} - 400}} = \frac{{45}}{{AH}}\\ \Leftrightarrow 40A{H^2} = 45A{H^2} - 18000\\ \Leftrightarrow A{H^2} = 3600\\ \Rightarrow AH = 60\end{array}\)
Bài 1.16 trang 19 SGK Toán 11 tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 1.16 trang 19 SGK Toán 11 tập 1 yêu cầu chúng ta xét hàm số bậc hai và xác định các yếu tố quan trọng của nó. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
- Định nghĩa hàm số bậc hai: Hàm số có dạng y = ax2 + bx + c, với a ≠ 0.
- Hệ số a: Xác định chiều mở của parabol (a > 0: mở lên, a < 0: mở xuống).
- Đỉnh của parabol: I(x0; y0), với x0 = -b/2a và y0 = f(x0).
- Trục đối xứng của parabol: Đường thẳng x = x0.
- Giao điểm với trục Oy: A(0; c).
- Giao điểm với trục Ox: Giải phương trình ax2 + bx + c = 0 để tìm hoành độ giao điểm.
Giải chi tiết Bài 1.16 trang 19 SGK Toán 11 tập 1
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử hàm số được cho là y = x2 - 4x + 3.
- Xác định hệ số a, b, c: a = 1, b = -4, c = 3.
- Xác định đỉnh của parabol: x0 = -(-4)/(2*1) = 2; y0 = 22 - 4*2 + 3 = -1. Vậy đỉnh của parabol là I(2; -1).
- Xác định trục đối xứng: x = 2.
- Xác định giao điểm với trục Oy: A(0; 3).
- Xác định giao điểm với trục Ox: Giải phương trình x2 - 4x + 3 = 0. Ta có nghiệm x1 = 1 và x2 = 3. Vậy giao điểm với trục Ox là B(1; 0) và C(3; 0).
Vẽ đồ thị hàm số
Dựa vào các yếu tố đã xác định, chúng ta có thể vẽ đồ thị hàm số y = x2 - 4x + 3. Đồ thị là một parabol có đỉnh I(2; -1), mở lên, trục đối xứng x = 2, đi qua các điểm A(0; 3), B(1; 0) và C(3; 0).
Lưu ý quan trọng
Khi giải các bài tập về hàm số bậc hai, cần chú ý:
- Kiểm tra kỹ các hệ số a, b, c.
- Tính toán chính xác tọa độ đỉnh và giao điểm.
- Vẽ đồ thị chính xác để hình dung rõ hơn về hàm số.
Bài tập tương tự
Để rèn luyện thêm kỹ năng, bạn có thể thử giải các bài tập tương tự với các hàm số khác. Ví dụ:
- y = -2x2 + 8x - 5
- y = 3x2 - 6x + 1
Kết luận
Bài 1.16 trang 19 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và đồ thị parabol. Bằng cách nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải bài tập, bạn sẽ học Toán 11 một cách hiệu quả hơn. tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức!