Bài 4.7 trang 100 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 4.7 trang 100 SGK Toán 11 tập 1 - Cùng khám phá
Bài 4.7 thuộc chương trình Toán 11 tập 1, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các quy tắc tính đạo hàm và cách áp dụng chúng vào việc tìm đạo hàm của hàm số.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AD và P, Q là hai điểm phân biệt cùng thuộc đường thẳng BC. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ.
Đề bài
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AD và P, Q là hai điểm phân biệt cùng thuộc đường thẳng BC. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ.
Phương pháp giải - Xem chi tiết
Hai đường thẳng chéo nhau là hai đường thẳng không đồng phẳng.
Lời giải chi tiết
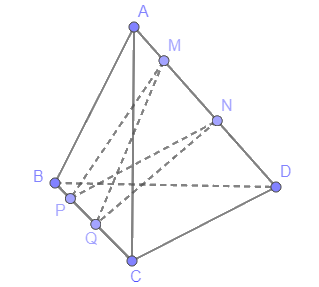
Giả sử MP và QN, MQ và PN cùng nằm trong một mặt phẳng. Suy ra M, P, Q, N thuộc cùng một mặt phẳng.
Mà M, N thuộc AD; P, Q thuộc BC. Nên AD, BC cũng cùng thuộc một mặt phẳng.
Tức là A, B, C, D đồng phẳng (Mâu thuẫn).
Vậy MP và QN chéo nhau, MQ và PN chéo nhau.
Bài 4.7 trang 100 SGK Toán 11 tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 4.7 trang 100 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 4.7 yêu cầu tính đạo hàm của các hàm số sau:
- a) y = x3 - 3x2 + 2x - 5
- b) y = (x2 + 1)(x - 2)
- c) y = (2x + 1) / (x - 3)
- d) y = sin(2x + 1)
Lời giải chi tiết
a) y = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
y' = 3x2 - 6x + 2
b) y = (x2 + 1)(x - 2)
Áp dụng quy tắc đạo hàm của tích, ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
c) y = (2x + 1) / (x - 3)
Áp dụng quy tắc đạo hàm của thương, ta có:
y' = [(2)(x - 3) - (2x + 1)(1)] / (x - 3)2 = (2x - 6 - 2x - 1) / (x - 3)2 = -7 / (x - 3)2
d) y = sin(2x + 1)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Hướng dẫn giải bài tập tương tự
Để giải các bài tập tương tự, bạn cần nắm vững các quy tắc đạo hàm cơ bản sau:
- Đạo hàm của tổng/hiệu: (u + v)' = u' + v'
- Đạo hàm của tích: (uv)' = u'v + uv'
- Đạo hàm của thương: (u/v)' = (u'v - uv') / v2
- Đạo hàm của hàm hợp: (f(g(x)))' = f'(g(x)) * g'(x)
Ngoài ra, bạn cần nhớ các đạo hàm cơ bản của các hàm số thường gặp như:
| Hàm số | Đạo hàm |
|---|---|
| xn | nxn-1 |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
Lưu ý: Khi tính đạo hàm, hãy chú ý đến thứ tự thực hiện các phép toán và áp dụng đúng các quy tắc đạo hàm. Thực hành nhiều bài tập khác nhau để làm quen với các dạng bài và nâng cao kỹ năng giải toán.
Hy vọng lời giải chi tiết và hướng dẫn này sẽ giúp bạn hiểu rõ hơn về Bài 4.7 trang 100 SGK Toán 11 tập 1. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại đặt câu hỏi tại tusach.vn!