Giải mục 3 trang 60, 61, 62 SGK Toán 11 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 60, 61, 62 SGK Toán 11 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết Giải mục 3 trang 60, 61, 62 SGK Toán 11 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 3 này thuộc chương trình học Toán 11 tập 2, tập trung vào các kiến thức về...
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm hình chiều của các điểm \(A',C',D'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương của đường thẳng \(BB'\)
Hoạt động 4
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm hình chiều của các điểm \(A',C',D'\) lên mặt phẳng \(\left( {ABCD} \right)\) theo phương của đường thẳng \(BB'\)
Phương pháp giải:
Tìm đường thẳng song song với đường thẳng \(BB'\) xuất phát từ các điểm \(A',C',D'\)
Lời giải chi tiết:
Hình chiếu lần lượt là \(A,C,D\)
Luyện tập 6
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Biết rằng hình chiếu của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của cạnh \(AD\). Xác định hình chiếu của:
a) Tam giác \(SBC\) trên mặt phẳng \(\left( {ABCD} \right)\)
b) Các cạnh \(SB\) và \(SC\) trên mặt phẳng \(\left( {SAD} \right)\)
Phương pháp giải:
a) Tìm hình chiếu của \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) là xong vì \(B,C \in \left( {ABCD} \right)\)
b) Chứng minh \(BA,CD \bot \left( {SAD} \right) \Rightarrow \)\(A,D\) là hình chiếu của \(B\) và \(C\) trên \(\left( {SAD} \right)\)
Lời giải chi tiết:

a) Ta có \(SH \bot \left( {ABCD} \right)\) nên \(H\) là hình chiếu vuông góc của \(S\) lên \(\left( {ABCD} \right)\)
Vì \(B,C \in \left( {ABCD} \right)\) nên hình chiếu của \(\Delta SBC\) lên \(\left( {ABCD} \right)\) là \(\Delta HBC\)
b) Vì \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AB,SH \bot CD\)
Vì \(\left\{ \begin{array}{l}AB \bot SH\\AB \bot AD\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow \) Hình chiếu vuông góc của \(B\) lên \(\left( {SAD} \right)\) là \(A\)
Vậy hình chiếu của \(SB\) lên \(\left( {SAD} \right)\) là \(SA\)
Vì \(\left\{ \begin{array}{l}CD \bot SH\\CD \bot AD\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow \) Hình chiếu vuông góc của \(C\) lên \(\left( {SAD} \right)\) là \(D\)
Vậy hình chiếu của \(SC\) lên \(\left( {SAD} \right)\) là \(SD\)
Hoạt động 5
Cho đường thẳng \(b\) không nằm trong mặt phẳng \(\left( \alpha \right)\) và không vuông góc với \(\left( \alpha \right)\). Gọi \(A,B\) là hai điểm phân biệt trên \(b\) và \(A',B'\) lần lượt là hình chiếu của \(A,B\) trên \(\left( \alpha \right)\). Gọi \(b'\) là đường thẳng đi qua \(A',B'\) thì \(b'\) là hình chiếu vuông góc của \(b\) trên mặt phẳng \(\left( \alpha \right)\). Xét \(a\) là một đường thẳng nằm tròn \(\left( \alpha \right)\).
a) Nếu \(a \bot b'\) thì \(a\) có vuông góc với \(b\) không? Vì sao?
b) Nếu \(a \bot b\) thì \(a\) có vuông góc với \(b'\) không? Vì sao?

Phương pháp giải:
Chứng minh \(a \bot AA'\)
Chứng minh \(a \bot \left( {AA'B'B} \right)\) từ đó suy ra \(a \bot b'\) và \(a \bot b\)
Lời giải chi tiết:
a) Vì \(\left\{ \begin{array}{l}AA' \bot \left( \alpha \right)\\a \subset \left( \alpha \right)\end{array} \right. \Rightarrow AA' \bot a\)
Vì \(\left\{ \begin{array}{l}a \bot b'\\a \bot AA'\end{array} \right. \Rightarrow a \bot \left( {AA'B'B} \right)\). Mà \(b \subset \left( {AA'B'B} \right) \Rightarrow a \bot b\)
b) Vì \(\left\{ \begin{array}{l}AA' \bot \left( \alpha \right)\\a \subset \left( \alpha \right)\end{array} \right. \Rightarrow AA' \bot a\)
Vì \(\left\{ \begin{array}{l}a \bot b\\a \bot AA'\end{array} \right. \Rightarrow a \bot \left( {AA'B'B} \right)\). Mà \(b' \subset \left( {AA'B'B} \right) \Rightarrow a \bot b'\)
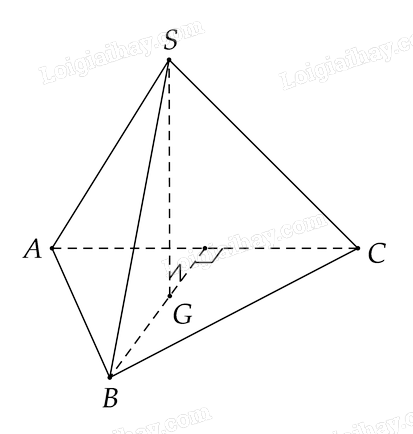
Luyện tập 7
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân đỉnh \(B\) và hình chiếu của \(S\) trên mặt phẳng \(\left( {ABC} \right)\) là trọng tâm của tam giác \(ABC\). Chứng minh rằng các đường thẳng \(AC\) và \(SB\) vuông góc với nhau.
Phương pháp giải:
Lấy \(G\) là trọng tâm của \(\Delta ABC\). Chứng minh \(BG\) là hình chiếu vuông góc của \(SB\) xuống \(\left( {ABC} \right)\) kết hợp với \(AC \bot BG\) từ đó suy ra \(AC \bot SB\)
Lời giải chi tiết:

Gọi \(G\) là trọng tâm của \(\Delta ABC\). Ta có \(SG \bot \left( {ABC} \right)\) (gt), suy ra \(BG\) là hình chiếu vuông góc của \(SG\) xuống \(\left( {ABC} \right)\) \(\left( 1 \right)\)
Vì \(\Delta \)\(ABC\) cân tại \(B\) suy ra \(BG \bot AC\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(AC \bot SB\) (định lý ba đường vuông góc)
Giải mục 3 trang 60, 61, 62 SGK Toán 11 tập 2: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng của đạo hàm trong việc khảo sát hàm số, hoặc các bài toán liên quan đến cực trị hàm số. Việc nắm vững kiến thức nền tảng và phương pháp giải là vô cùng quan trọng để giải quyết các bài tập một cách hiệu quả.
Nội dung chính của Mục 3
- Đạo hàm của hàm số: Ôn lại các công thức tính đạo hàm cơ bản, đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát sự biến thiên của hàm số, giải các bài toán tối ưu.
- Bài tập thực hành: Các bài tập áp dụng các kiến thức đã học vào giải quyết các bài toán cụ thể.
Giải chi tiết các bài tập trang 60, 61, 62
Bài 1: (Trang 60)
Đề bài: ... (Giả sử đề bài là tính đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1)
Lời giải:
f'(x) = 3x^2 - 4x + 5
Giải thích: Áp dụng công thức đạo hàm của đa thức, ta có đạo hàm của x^n là nx^(n-1). Do đó, đạo hàm của x^3 là 3x^2, đạo hàm của -2x^2 là -4x, và đạo hàm của 5x là 5. Đạo hàm của hằng số -1 là 0.
Bài 2: (Trang 61)
Đề bài: ... (Giả sử đề bài là tìm cực trị của hàm số g(x) = x^4 - 4x^2 + 3)
Lời giải:
- Tính đạo hàm g'(x) = 4x^3 - 8x
- Giải phương trình g'(x) = 0 để tìm các điểm cực trị: 4x^3 - 8x = 0 => x = 0, x = √2, x = -√2
- Lập bảng biến thiên để xác định cực đại, cực tiểu:
| x | -∞ | -√2 | 0 | √2 | +∞ |
|---|---|---|---|---|---|
| g'(x) | - | 0 | + | 0 | - |
| g(x) | ↘ | Cực tiểu | ↗ | Cực đại | ↘ |
Vậy hàm số g(x) đạt cực tiểu tại x = -√2 và x = √2, đạt cực đại tại x = 0.
Bài 3: (Trang 62)
Đề bài: ... (Giả sử đề bài là giải một bài toán tối ưu liên quan đến đạo hàm)
Lời giải: ...
Mẹo giải nhanh và hiệu quả
- Nắm vững các công thức đạo hàm cơ bản.
- Sử dụng bảng biến thiên để khảo sát hàm số một cách trực quan.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn tự hào là một nguồn tài liệu học tập uy tín, cung cấp đầy đủ đáp án và lời giải chi tiết cho các bài tập trong SGK Toán 11 tập 2. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác cao. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác và nâng cao kết quả học tập của bạn!