Bài 8.22 Trang 79 SGK Toán 11 Tập 2

Bài 8.22 trang 79 SGK Toán 11 tập 2 - Cùng khám phá

Bài 8.22 thuộc chương trình Toán 11 tập 2, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ các công thức đạo hàm cơ bản và kỹ năng áp dụng chúng vào việc tìm đạo hàm của hàm số.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu cùng với các phương pháp giải khác nhau để giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ A đến (BCD).

Đề bài

Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ A đến (BCD).

Phương pháp giải - Xem chi tiết Bài 8.22 trang 79 SGK Toán 11 tập 2 - Cùng khám phá 1

Tìm khoảng cách giữa M và (P):

+ Tìm (Q) chứa M và vuông góc với (P) theo giao tuyến d.

+ Từ M hạ MH vuông góc với d (H thuộc d).

+ Khi đó MH là khoảng cách cần tìm.

Lời giải chi tiết

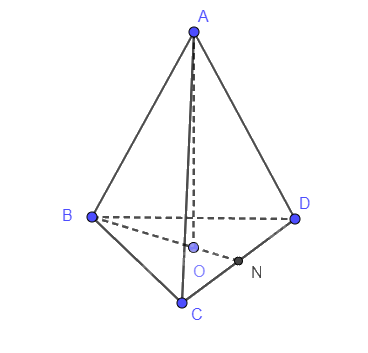
Bài 8.22 trang 79 SGK Toán 11 tập 2 - Cùng khám phá 2

Gọi N là trung điểm CD, AO vuông góc với BN

AO vuông góc với (BCD) nên O là trọng tâm tam giác BCD

Vậy khoảng cách cần tìm là AO

\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {{a^2} - \frac{{3{a^2}}}{9}} = \frac{{a\sqrt 6 }}{3}\)

Bài 8.22 Trang 79 SGK Toán 11 Tập 2: Giải Chi Tiết và Phân Tích

Bài 8.22 trang 79 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bài tập này thường yêu cầu học sinh tính đạo hàm của một hàm số hoặc giải một phương trình liên quan đến đạo hàm.

Nội dung bài tập 8.22 trang 79 SGK Toán 11 tập 2

Thông thường, bài 8.22 sẽ đưa ra một hàm số cụ thể và yêu cầu tính đạo hàm của hàm số đó. Đôi khi, bài tập cũng có thể yêu cầu tìm các điểm cực trị của hàm số hoặc giải một phương trình đạo hàm.

Phương pháp giải bài 8.22 trang 79 SGK Toán 11 tập 2

Để giải bài 8.22 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

Các công thức đạo hàm cơ bản: Đạo hàm của các hàm số đơn giản như xⁿ, sin(x), cos(x), e^x, ln(x),...
Các quy tắc đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc chuỗi,...
Kỹ năng biến đổi đại số: Để đơn giản hóa biểu thức trước khi tính đạo hàm.

Lời giải chi tiết bài 8.22 trang 79 SGK Toán 11 tập 2 (Ví dụ minh họa)

Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = 2x³ + 3x² - 5x + 1.

Áp dụng quy tắc đạo hàm của tổng: f'(x) = (2x³)' + (3x²)' - (5x)' + (1)'
Áp dụng quy tắc đạo hàm của lũy thừa: f'(x) = 6x² + 6x - 5 + 0
Kết quả: f'(x) = 6x² + 6x - 5

Các dạng bài tập tương tự và cách giải

Ngoài bài 8.22, còn rất nhiều bài tập tương tự yêu cầu tính đạo hàm của các hàm số phức tạp hơn. Để giải các bài tập này, bạn cần:

Sử dụng quy tắc chuỗi: Khi đạo hàm của một hàm hợp.
Sử dụng đạo hàm của các hàm lượng giác: Khi đạo hàm của các hàm số chứa sin, cos, tan,...
Sử dụng đạo hàm của hàm mũ và hàm logarit: Khi đạo hàm của các hàm số chứa e^x, ln(x),...

Mẹo giải nhanh bài tập về đạo hàm

Để giải nhanh các bài tập về đạo hàm, bạn có thể:

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính bỏ túi có chức năng tính đạo hàm. (Tuy nhiên, cần hiểu rõ bản chất của bài toán để sử dụng máy tính một cách hiệu quả).

Tài liệu tham khảo hữu ích

Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:

Sách giáo khoa Toán 11 tập 2
Sách bài tập Toán 11 tập 2
Các trang web học Toán trực tuyến như tusach.vn
Các video bài giảng Toán 11 trên YouTube

Kết luận

Bài 8.22 trang 79 SGK Toán 11 tập 2 là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Bằng cách nắm vững các công thức đạo hàm cơ bản, quy tắc đạo hàm và kỹ năng biến đổi đại số, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự.