Giải mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 3 này tập trung vào các kiến thức quan trọng của chương trình Toán 11, do đó việc nắm vững nội dung là vô cùng cần thiết.
Bánh ít lá gai là một đặc sản của người miền Trung, có dạng là một hình chóp tứ giác như Hình 4.29a.
Hoạt động 7
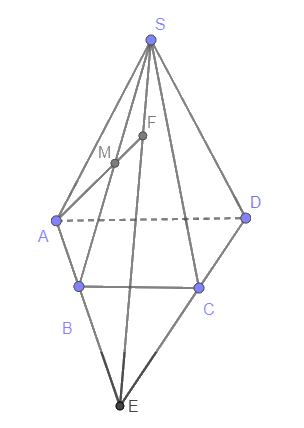
Bánh ít lá gai là một đặc sản của người miền Trung, có dạng là một hình chóp tứ giác như Hình 4.29a. Trong không gian, hình ảnh bánh ít lá gai có thể biểu diễn bởi Hình 4.29b. Hãy gọi tên các tam giác và tứ giác ở Hình 4.29b tương ứng với các bề mặt được gói lá của một chiếc bánh ít.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Các tam giác trong Hình 4.29b là SAC, SAD, SAB, SCD.
Tứ giác trong Hình 4.29b là ABCD.
Luyện tập 6
Cho hình chóp S.ABCD với hai đường thẳng AB và CD cắt nhau. Gọi M là một điểm thuộc SA (khác S và A). Hãy tìm các giao tuyến của mặt phẳng (MCD) với các mặt phẳng (ABCD), (SAB), (SCD), (SBC), (SAD).
Phương pháp giải:
Tìm giao tuyến của hai mặt phẳng (P) và (Q):
Tìm điểm chung A, B của 2 mặt phẳng đó. Đường thẳng AB là giao tuyến cần tìm.
Chú ý: Thường tìm 2 đường đồng phẳng lần lượt nằm trong (P) và (Q) (nếu có). 2 đường đó cắt nhau tại điểm nào thì đó là điểm chung của hai mặt phẳng.
Lời giải chi tiết:

Trong (ABCD), gọi E là giao điểm của AB và CD
Trong (SAB), gọi N là giao điểm của EM và SB
\(\left( {MCD} \right) \cap \left( {ABCD} \right) = CD\)
\(\left( {MCD} \right) \cap \left( {SCD} \right) = CD\)
\(\left( {MCD} \right) \cap \left( {SAD} \right) = DM\)
\(\begin{array}{l}E = AB \cap CD\\\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\CD \subset \left( {MCD} \right)\\M \in SA\end{array} \right.\\ \Rightarrow \left( {MCD} \right) \cap \left( {SAB} \right) = EM\end{array}\)
Mở rộng (MCD) thành (MEC)
\(\begin{array}{l}N = EM \cap SB\\\left\{ \begin{array}{l}SB \subset \left( {SBC} \right)\\EM \subset \left( {MEC} \right)\end{array} \right.\\ \Rightarrow \left( {MEC} \right) \cap \left( {SBC} \right) = CN \Leftrightarrow \left( {MCD} \right) \cap \left( {SBC} \right) = CN\end{array}\)
Hoạt động 8
Trong hoá học, ta đã biết phân tử khí methane (CH) có một nguyên tử carbon (C) liên kết với bốn nguyên tử hydrogen (H) và các nguyên tử này không cùng nằm trong một mặt phẳng. Nếu xem bốn nguyên tử hydrogen là bốn điểm A, B, C, D thì ta có bao nhiêu tam giác khác nhau tạo từ bốn điểm này? (Nguồn: https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_( LibreTexts)/01%3A_Structure_ and Bonding/1.06 %3A_sp_Hybrid_Orbitals_and_the_Structure_of_Methane)

Phương pháp giải:
Cứ 3 điểm bất kì không thẳng hàng thì tạo thành một tam giác.
Lời giải chi tiết:
Nếu xem bốn nguyên tử hydrogen là bốn điểm A, B, C, D thì 4 điểm này tạo thành 4 tam giác khác nhau là ABC, ABD, ACD, BCD.
Luyện tập 7
Cho hình chóp S.ABCD với ABCD là hình thang có đáy lớn là AB. Gọi M là trung điểm của SD. Hãy xác định giao tuyến của các cặp mặt phẳng: (SAD) và (SBC), (MBC) và (SAD).
Phương pháp giải:
Tìm giao tuyến của hai mặt phẳng (P) và (Q):
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
Chú ý: Thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong (P) và (Q). Nếu chúng cắt nhau tại 1 điểm thì đó là điểm chung của (P) và (Q).
Lời giải chi tiết:

Trong (ABCD), gọi \(AD \cap BC = E\)
\(\begin{array}{l}\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\BD \subset \left( {SBD} \right)\end{array} \right.\\ \Rightarrow \left( {SAD} \right) \cap \left( {SBD} \right) = SE\end{array}\)
\(\begin{array}{l}AD \cap BC = E\\\left\{ \begin{array}{l}AD \subset \left( {SAC} \right)\\BC \subset \left( {MBC} \right)\\M \in SD\end{array} \right.\\ \Rightarrow \left( {MBC} \right) \cap \left( {SAD} \right) = EM\end{array}\)
Luyện tập 8
Trong mặt phẳng (Q), cho hình thang ABCD có đáy lớn là AD. Lấy điểm S nằm ngoài mặt phẳng (Q). Gọi M là trung điểm của SB. Tìm giao điểm của đường thẳng AM và mặt phẳng (SCD).
Phương pháp giải:
Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng a cắt d

Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)
Lời giải chi tiết:
Trong (ABCD), gọi \(AB \cap DC = E\)
\(\begin{array}{l}\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\DC \subset \left( {SDC} \right)\end{array} \right.\\ \Rightarrow \left( {SAB} \right) \cap \left( {SDC} \right) = SE\end{array}\)
Trong (SAE), gọi \(SE \cap AM = N\)
Mà: \(AM \subset \left( {SAB} \right)\)
\( \Rightarrow N = AM \cap \left( {SCD} \right)\)
Vận dụng 2
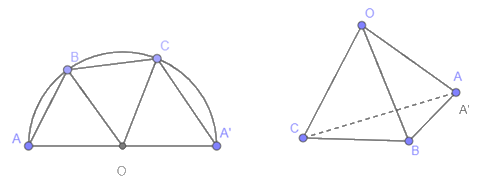
Cắt một miếng bìa thành nửa hình tròn tâm O, đường kính AA’. Trên cung AA’, lấy hai điểm B, C bất kì (khác A, A’). Dùng kéo cắt theo các đường AB, BC, CA’ sau đó gấp giấy theo các đường OB, OC và dán hai mép , OA’ lại với nhau. Khi đó, ta được một mô hình của hình chóp (không có mặt đáy).
a) Hình chóp này có tên gọi là gì?
b) Bằng cách làm này, muốn có một hình chóp lục giác (không đáy) thì ta cần lấy bao nhiều điểm trên cung AA’?
Phương pháp giải:
Hình chóp tam giác đều là hình có các mặt bên là tam giác cân và đáy là tam giác đều.
Lời giải chi tiết:

a) Sau khi ghép theo đề bài, ta được hình chóp tam giác đều vì 3 cạnh bên OA = OB = OC (cùng bằng bán kính đường tròn tâm O), AB = BC = CA’ nên có đáy là tam giác đều.
b) Theo phần a, để được hình chóp tam giác đều (không đáy) thì ta lấy 2 điểm trên cung AA’. Nên để được hình chóp lục giác (không đáy) thì ta lấy 4 điểm trên cung AA’.
Giải mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1 - Cùng khám phá
Mục 3 của SGK Toán 11 tập 1 thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc hiểu rõ các tính chất và ứng dụng của các phép biến hình này là nền tảng quan trọng cho các kiến thức toán học nâng cao hơn.
Nội dung chính của mục 3
- Phép tịnh tiến: Định nghĩa, tính chất, và cách thực hiện phép tịnh tiến trong mặt phẳng.
- Phép quay: Định nghĩa, tính chất, và cách thực hiện phép quay quanh một điểm cho trước.
- Phép đối xứng trục: Định nghĩa, tính chất, và cách thực hiện phép đối xứng qua một đường thẳng.
- Phép đối xứng tâm: Định nghĩa, tính chất, và cách thực hiện phép đối xứng qua một điểm.
- Bài tập vận dụng: Các bài tập giúp học sinh rèn luyện kỹ năng và hiểu sâu hơn về các phép biến hình.
Giải chi tiết bài tập trang 90, 91, 92, 93
Dưới đây là giải chi tiết các bài tập trong mục 3, trang 90, 91, 92, 93 SGK Toán 11 tập 1:
Bài 1: (Trang 90)
Đề bài: Cho điểm A(1; 2) và vector v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vector v.
Giải: Tọa độ điểm A' được tính theo công thức: A'(xA + xv; yA + yv) = (1 + 3; 2 - 1) = (4; 1).
Bài 2: (Trang 91)
Đề bài: Cho điểm B(-2; 3) và góc quay α = 90o. Tìm tọa độ điểm B' là ảnh của B qua phép quay tâm O(0; 0) góc α.
Giải: Sử dụng công thức phép quay: B'(xBcosα - yBsinα; xBsinα + yBcosα) = (-2cos90o - 3sin90o; -2sin90o + 3cos90o) = (-3; -2).
Bài 3: (Trang 92)
Đề bài: Tìm phương trình đường thẳng d' là ảnh của đường thẳng d: x + 2y - 3 = 0 qua phép đối xứng trục Ox.
Giải: Phép đối xứng trục Ox biến điểm M(x; y) thành M'(x; -y). Do đó, phương trình đường thẳng d' là x + 2(-y) - 3 = 0, hay x - 2y - 3 = 0.
Bài 4: (Trang 93)
Đề bài: Tìm tọa độ điểm C' là ảnh của điểm C(4; -1) qua phép đối xứng tâm I(1; 2).
Giải: Tọa độ điểm C' được tính theo công thức: C'(2xI - xC; 2yI - yC) = (2*1 - 4; 2*2 - (-1)) = (-2; 5).
Lưu ý khi giải bài tập
- Nắm vững định nghĩa và tính chất của từng phép biến hình.
- Sử dụng đúng công thức để tính toán tọa độ điểm và phương trình đường thẳng.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1 và tự tin hơn trong quá trình học tập. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!