Logo

Bài 4.33 trang 124 SGK Toán 11 tập 1 - Cùng khám phá

Tổng quan nội dung

Bài 4.33 Trang 124 SGK Toán 11 Tập 1: Cùng Khám Phá

Bài 4.33 trang 124 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải quyết bài toán.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán hiệu quả.

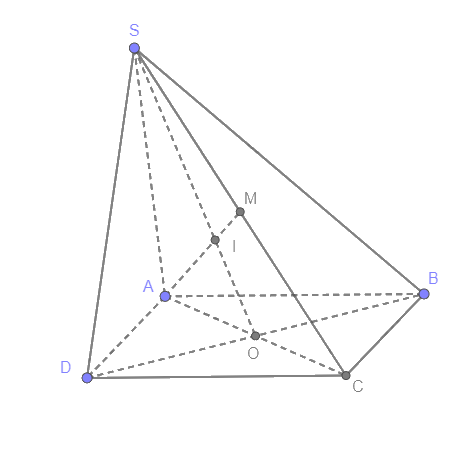
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SC. Gọi I là giao điểm của dường thẳng AM và mặt phẳng (SBD). Mệnh đề nào sau đây đúng?

Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SC. Gọi I là giao điểm của dường thẳng AM và mặt phẳng (SBD). Mệnh đề nào sau đây đúng?

A. IA = 3IM.

B. IM = 3IA.

C. IM = 2IA.

D. IA = 2IM.

Phương pháp giải - Xem chi tiếtBài 4.33 trang 124 SGK Toán 11 tập 1 - Cùng khám phá 1

Cách tìm giao điểm của đường thẳng a và mặt phẳng (P):

+ Bước 1: Chọn mặt phẳng (Q) chứa a. Tìm giao tuyến d của (P) và (Q)

+ Bước 2: Tìm giao điểm I của a và d. I chính là giao điểm của d và (P).

Lời giải chi tiết

Bài 4.33 trang 124 SGK Toán 11 tập 1 - Cùng khám phá 2

Trong (ABCD), gọi O là giao điểm của AC và BD

Trong (SAC), gọi I là giao điểm của AM và SO

Mà SO nằm trong (SBD) nên I là giao điểm của AM và (SBD)

Hình bình hành ABCD có O là giao điểm của AC và BD nên O là trung điểm AC, BD

Xét tam giác SAC có AM, SO là trung tuyến nên I là trọng tâm

Vậy IA = 2IM

Chọn đáp án D.

Bài 4.33 Trang 124 SGK Toán 11 Tập 1: Giải Chi Tiết và Phân Tích

Bài 4.33 trang 124 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phân tích bài toán này:

Nội dung Bài Toán

(Giả sử nội dung bài toán là: Cho hàm số y = f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)

Lời Giải Chi Tiết

  1. Bước 1: Tìm tập xác định của hàm số.

    2. Hàm số y = f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.

  2. Bước 2: Tính đạo hàm cấp nhất f'(x).

    3. f'(x) = 3x2 - 6x

  3. Bước 3: Tìm các điểm dừng của hàm số.

    4. Giải phương trình f'(x) = 0:

    3x2 - 6x = 0

    3x(x - 2) = 0

    Suy ra x = 0 hoặc x = 2

  4. Bước 4: Lập bảng biến thiên.
    5. x-∞02+∞
    f'(x)+-+
    f(x)↗↘↗
  5. Bước 5: Kết luận.

    6. Dựa vào bảng biến thiên, ta thấy:

    • Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
    • Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.

Lưu Ý Quan Trọng

Khi giải các bài toán về cực trị của hàm số, cần lưu ý các bước sau:

  • Xác định đúng tập xác định của hàm số.
  • Tính đạo hàm cấp nhất một cách chính xác.
  • Giải phương trình đạo hàm bằng nhất để tìm các điểm dừng.
  • Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.

Ứng Dụng Của Đạo Hàm Trong Thực Tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:

  • Trong kinh tế: Tính toán chi phí biên, doanh thu biên, lợi nhuận biên.
  • Trong vật lý: Tính vận tốc, gia tốc, lực.
  • Trong kỹ thuật: Tối ưu hóa thiết kế, điều khiển hệ thống.

Bài Tập Tương Tự

Để rèn luyện thêm kỹ năng giải toán về đạo hàm, bạn có thể tham khảo các bài tập tương tự sau:

  • Bài 4.34 trang 124 SGK Toán 11 tập 1
  • Bài 4.35 trang 125 SGK Toán 11 tập 1

Chúc bạn học tốt!

Mọi thắc mắc về bài 4.33 trang 124 SGK Toán 11 tập 1, hãy để lại bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ bạn.