Bài 4.6 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Tổng quan nội dung
Bài 4.6 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Bài 4.6 thuộc chương trình Toán 11 tập 1, tập trung vào việc ôn tập về đường thẳng và mặt phẳng trong không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
Đề bài
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
a) Tim giao tuyến của hai mặt phẳng (SBG) và (SAC).
b) Tìm giao điểm của đường thằng BG và mặt phẳng (SAC).
Phương pháp giải - Xem chi tiết
a) Tìm giao tuyến của hai mặt phẳng (P) và (Q)
Tìm 2 điểm chung A, B của 2 mặt phẳng đó. AB chính là giao tuyến của (P) và (Q).
b) Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng cắt d
Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)
Lời giải chi tiết
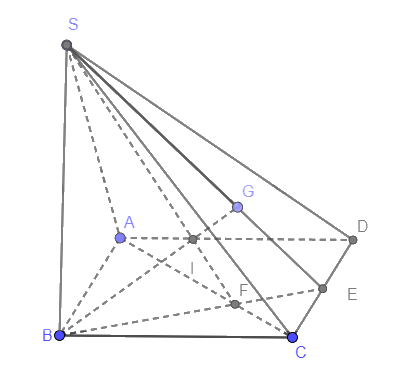
a) Gọi E là trung điểm của CD
Mà G là trọng tâm tam giác SCD nên G nằm trên SE.
Mở rộng (SBG) thành (SBE)
Trong (ABCD), gọi \(AC \cap BE = F\)
\(\begin{array}{l}\left\{ \begin{array}{l}AC \subset \left( {SAC} \right)\\BE \subset \left( {SBE} \right)\end{array} \right.\\ \Rightarrow F \in \left( {SAC} \right) \cap \left( {SBE} \right)\end{array}\)
\(\begin{array}{l} \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBE} \right)\\ \Rightarrow SF = \left( {SAC} \right) \cap \left( {SBG} \right)\end{array}\)
b) Trong (SBE), gọi \(SF \cap AC = I\)
Mà: \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {SBG} \right) = SF\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow I = BG \cap \left( {SAC} \right)\)
Bài 4.6 Trang 94 SGK Toán 11 Tập 1 - Cùng khám phá: Giải chi tiết và hướng dẫn
Bài 4.6 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập
Bài 4.6 yêu cầu học sinh xác định vị trí tương đối giữa đường thẳng và mặt phẳng, hoặc chứng minh một đường thẳng song song với một mặt phẳng. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa về đường thẳng song song với mặt phẳng.
- Điều kiện để đường thẳng song song với mặt phẳng.
- Cách xác định giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết
(Ở đây sẽ là lời giải chi tiết cho bài 4.6, bao gồm các bước giải, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác. Ví dụ:)
Ví dụ: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng SM song song với mặt phẳng (ABD).
- Phân tích: Để chứng minh SM song song với (ABD), ta cần chứng minh SM song song với một đường thẳng nằm trong (ABD).
- Cách giải:
- Gọi N là trung điểm của cạnh CD.
- Chứng minh MN song song với BD (theo định lý đường trung bình của tam giác BCD).
- Chứng minh SM song song với MN (do MN nằm trong (ABD)).
- Suy ra SM song song với (ABD).
Các dạng bài tập tương tự
Ngoài bài 4.6, còn rất nhiều bài tập tương tự về vị trí tương đối giữa đường thẳng và mặt phẳng. Dưới đây là một số dạng bài tập thường gặp:
- Xác định vị trí tương đối giữa hai đường thẳng.
- Xác định vị trí tương đối giữa hai mặt phẳng.
- Chứng minh một đường thẳng vuông góc với một mặt phẳng.
Mẹo giải bài tập
Để giải các bài tập về đường thẳng và mặt phẳng một cách hiệu quả, bạn nên:
- Vẽ hình minh họa rõ ràng.
- Nắm vững các định nghĩa và tính chất cơ bản.
- Sử dụng các phương pháp chứng minh phù hợp (ví dụ: phương pháp tọa độ, phương pháp hình học).
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tài liệu tham khảo
Để học tập và ôn luyện kiến thức về đường thẳng và mặt phẳng, bạn có thể tham khảo các tài liệu sau:
- Sách giáo khoa Toán 11 tập 1.
- Sách bài tập Toán 11 tập 1.
- Các trang web học Toán trực tuyến uy tín (ví dụ: tusach.vn).
Kết luận
Bài 4.6 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.